习题6－8

习题6－8

1.求下列各微分方程的通解.

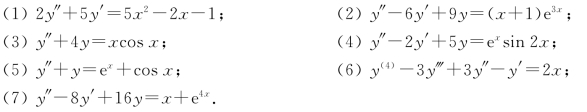
2.求解下列初始问题.

（1）y″－10y′＋9y＝e2x，y｜x＝0＝，y′｜x＝0＝

（2）y″－y＝4xex，y｜x＝0＝0，y′｜x＝0＝1；

（3）y″＋y＝cos 2x，y｜＝1，y′｜＝1.x＝0x＝0

3.已知y1＝xex＋e2x，y2＝xex＋e－x，y3＝xex＋e2x－e－x是二阶线性非齐次方程的三个解，求此微分方程.

4.求微分解方程y″－2y′＝f（x）的一个特解，其中系数f（x）分别等于：

（1）1－6x2； （2）xex； （3）4xe2x.

5.设对于x＞0，曲线y＝f（x）上点（x，f（x））处的切线在y轴上的截距等于f（t）dt，求f（x）的一般表达式.

6.若连续函数φ（x）满足φ（x）＝ex＋（t－x）φ（t）dt，求φ（x）.

7.利用代换y＝，将方程

y″cos x－2y′sin x＋3ycos x＝ex

化简，并求出原方程的通解.