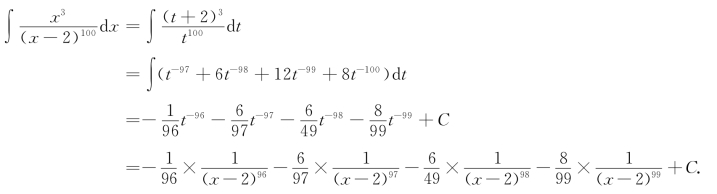有理函数的不定积分
设p（x），θ（x）均为多项式函数，凡形如的函数称为有理函数，若分子次数严格低于分母的次数，则称它为真分式，否则称它为假分式.由于假分式总可化为一个多项式与一个真分式之和，因此只需研究真分式的积分法即可.
由代数学的知识可知，多项式在实数范围内总可分解成形如x－a的一次不可约因式与形如x2＋px＋q（p2－4q＜0）的二次不可约因式之积，且将分母作此种分解后，真分式总可以表示成相应的一些部分分式之和.如果分母含有形如（x－a）k的因式，则对应的部分分式是
如果分母含有形如（x2＋px＋q）n的因式，则对应的部分分式是
将真分式等于其对应的部分分式之和，通分后分母必相等.再通过分子相等，从而对应的同次幂系数相等，求出待定的常数（如Ai，Bi，Ci等）.这样便求出了真分式的所有部分分式.
例1 将
分解为部分分式之和.
解 将分母分解因式为
x5－x4＋2x3－2x2＋x－1＝（x－1）（x2＋1）2，
则x－1对应部分分式为
，（x2＋1）2对应部分分式为
令
右边通分后分子相同，得
2x＋2＝A（x2＋1）2＋（B1x＋C1）（x－1）（x2＋1）＋（B2x＋C2）（x－1）.
以下需求待定的系数A，B1，C1，B2，C2.
（方法一） 由于式中左右两端同次项系数相同，得线性方程组
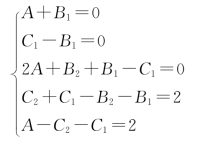
解此方程组，得
A＝1，B1＝－1，C1＝－1，B2＝－2，C2＝0.
（方法二） 取一些特殊点代入通分后的公式.
将x＝1代入，得4A＝4，即A＝1；将x＝i代入，得2i＋2＝（B2i＋C2）（i－1），从而有B2＝－2，C2＝0；将x＝0代入，得2＝A－C1－C2，则C1＝－1；将x＝－1代入，得0＝4A－4（C1－B1）－2（C2－B2），从而有B1＝－1.
由以上两种方法均求得
完成了部分分式的分解，只需求所有部分分式的积分.实际上，只需求以下两种形式的积分：
①∫
②∫
dx（p2－4q＜0）.
形式①积分较容易，即
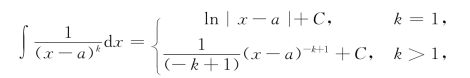
形式②积分时，其将分母代为平方和的幂，即
上式右边第一个积分
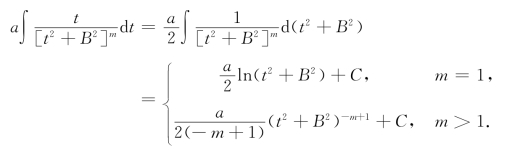
上式右边第二个积分可由第二节例19的递推公式求出.
这便完成了形式②的积分的计算.因此，综合以上理论，可得有理函数不定积分的一般方法.
例2 求∫
解 由1＋x3＝（1＋x）（1－x＋x2）可以求得部分分式分解，即
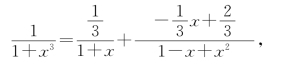
从而有
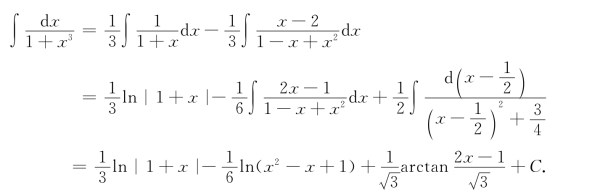
用常规的方法求不定积分不一定最简便.例3若用上述方法求解，过程会相当麻烦，因而可寻求更简便的方法.
例3 求∫
解 设x－2＝t，则x＝2＋t，dx＝dt，于是
