总习题二
1.填空题
（1）曲线y＝x－
在点
处的法线与直线y＝x平行.
（2）设f（x）为偶函数，且f′（0）存在，则f′（0）
（3）设f（x）在x＝1处连续，且
，则f′（1）
（4）已知y＝xx2＋2xx，则
（5）设y＝f（x＋y），其中f具有二阶导数，且y′≠1，则
（6）设y＝f（x）在x＝1处可导，且当h→0时，有f（1＋ln（1＋2h））＝2＋4h＋o（h），则曲线y＝f（x）在点（1，f（1））处的切线方程为
（7）设f（x）＝
，则
2.选择题
（1）设f（x）＝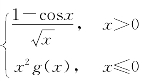
，其中g（x），有界则f（x）在x＝0处（ ）.
（A）极限不存在 （B）极限存在，但不连续
（C）连续，但不可导 （D）可导
（2）设f（a）＝2，f′（a）＝3，则
＝（ ）.
（A）18 （B）36 （C）9 （D）12
（3）设f（x）在x＝0连续，又
＝1，则（ ）.
（A）f（x）在x＝0可导，且f′（0）＝0 （B）f（x）在x＝0可导，且f′（0）≠0
（C）f′＋（0），f′－（0）均存在，但f′＋（0）≠f′－（0） （D）f′＋（0），f′－（0）均不存在
（4）设F（x）＝f（x）g（x），x＝a是g（x）的跳跃型间断点，f′（a）存在，则f（a）＝0，f′（a）＝0是F（x）在x＝a可导的（ ）.
（A）充分必要条件 （B）充分非必要条件
（C）必要非充分条件 （D）非充分非必要条件
3.已知f（x）＝｜x－a｜g（x），g（x）在x＝a连续，讨论f（x）在x＝a处的可导性.
4.若f′（3）＝2，求
5.若f′（a）＝b，求
6.若f（1）＝1，f′（1）＝2，f″（1）＝3，f‴（1）＝4，求
7.设f（u）在u＝t处可导，求
8.设f（x）在x＝1处有连续导数，且f′（1）＝2，求
9.设f（x）＝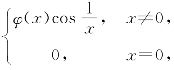
且（0）＝′（0）＝0，求f′（0）.φφ
10.设f（x）＝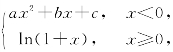
问：如何选择a，b，c，才能使f（x）处处具有一阶连续导数，但在x＝0处却不存在二阶导数？
11.求下列函数的导数.
（1）y＝xx2＋2xx； （2）y＝
，a＞0，b＞0；
（3）y＝xxa＋xax＋axx；（4）y＝2｜sin x｜；
（5）y＝arccos
12.设y＝y（x）由
所确定，求
13.已知y＝f（
），f′（x）＝arctan x2，求
14.设y＝sin［f（x2）］，其中f具有二阶导数，求
15.已知exy＝axby，证明：（y－ln a）y″－2（y′）2＝0.
16.设曲线y＝xn（n为正整数）上点（1，1）处的切线交x轴于（ξ，0），求
y（ξ）.