一、引例

一、引例

下面通过几何、力学及物理学中的几个具体例子说明微分方程的基本概念.

例1 一曲线通过点（1，），且在该曲线上任一点M（x，y）处的切线斜率为x2，求曲线的方程.

解 设所求曲线的方程为y＝y（x）.根据所给条件，应满足

将（1）式两端积分，得

即

其中C为任意常数.

把条件（2）式代入（3）式，得＋C，C＝1.

即得所求曲线方程为

例2 质量为m的物体以初速度v0自高为H处自由下落，求物体下落的距离h与时间t的函数关系（设物体下落时不计空气阻力）.

解 设变量h的正方向与速度及物体下落加速度的正方向一致，取作垂直向下，原点O距地面为H，设经过t秒后下落距离h与t的函数关系为h＝h（t），如图6－1所示.

由牛顿第二定律知

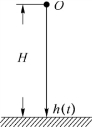
图6－1

且h（t）还满足

将（4）式两端对t积分，整理得

再对t积分一次得

其中C1，C2为任意常数.

将条件（5）式和（6）式代入（8）式，得C1＝v0，C2＝0，

因此物体经过t秒后下落的距离为