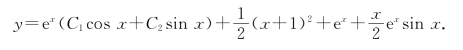f（x）＝Pm（x）eαxcosβx或f（x）＝Pm（x）eαxsinβx（其中α，β为实数）
令λ＝α＋iβ，设y＊＝Q（x）eλx是方程
y″＋py′＋qy＝Pm（x）eλx
的特解，则y＊的实部和虚部分别是方程
y″＋py′＋qy＝Pm（x）eαxcosβx
和方程
y″＋py′＋qy＝Pm（x）eαxsinβx
的特解.具体地说，如果Q（x）＝Q1（x）＋i Q2（x），其中Q1（x），Q2（x）为实函数，则
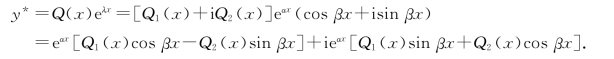
因此
y″＋py′＋qy＝Pm（x）eαxcosβx
的特解为
而方程
y″＋py′＋qy＝Pm（x）eαxsinβx
的特解为
也可以直接把（7）式、（8）式形式解代入方程求特解.
类似前面讨论，也可以直接设出此时非齐次方程的特解形式.
考虑方程
其中Am（x），Bn（x）分别是m次，n次多项式函数.则可设方程（9）的特解为
其中k取决于α＋iβ为特征方程（6）的k重根，l＝max｛m，n｝，Ql（x）和Pl（x）是两组带有待定系数的l次多项式函数.
例3 求方程y″＋y＝4sin x的通解.
解 特征方程φ（r）＝r2＋1，特征根r＝±i，故对应齐次方程的通解为
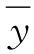＝C1cos x＋C2sin x，其中C1，C2为任意常数.
由于±i是特征根，设特解为y＊＝x（Asin x＋Bcos x），于是
（y＊）′＝（Acos x－Bsin x）x＋（Asin x＋Bcos x），（y＊）″＝（－Asin x－Bcos x）x，代入原方程可得
2Acos x－2Bsin x＝4sin x＋2（Acos x－Bsin x），
解得A＝0，B＝－2，
故
y＊＝－2xcos x
为所求非齐次方程特解.
所以原方程的通解为
y＝C1cos x＋C2sin x－2xcos x.
例4 求方程y″－2y′＋2y＝x2＋2excos2
的通解.
解 f（x）＝x2＋2excos2
＝x2＋ex＋excos x，由线性微分方程解的叠加原理，可设原方程特解为y＊＝
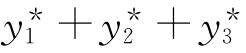，其中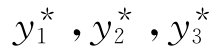
分别是对应非齐次项为x2，ex，excos x方程的特解.
特征方程φ（r）＝r2－2r＋2，特征根r1，2＝1±i，对应齐次方程通解为
（1）对于
y″－2y′＋2y＝x2，
0不是特征根，设特解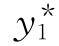
＝ax2＋bx＋c，则
代入方程，比较系数得
于是
（2）对于
y″－2y′＋2y＝ex，
1不是特征根，设特解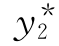
＝Aex，则
代入方程，比较系数得
A＝1，
可得
（3）对于
y″－2y′＋2y＝excos x，
1±i是特征根，设特解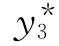
＝xex（Bcos x＋Dsin x），则
（
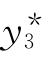）′＝（1＋x）ex（Bcos x＋Dsin x）＋xex（Dcos x－Bsin x），
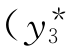）″＝（2＋x）ex（Bcos x＋Dsinx）＋2（1＋x）ex（Dcos x－Bsin x）＋xex（－Dsin x－Bcos x），
代入方程，比较系数得
可得
为方程
y″－2y′＋2y＝excos x
的一个特解.所以原方程的通解为
