三、函数的运算
函数之间的加、减、乘、除运算称为函数的四则运算，除此之外，还可以对函数进行复合运算、反函数运算，由此可以产生更多的函数.
1.复合函数
定义2 设y＝f（u）的定义域为Df，值域为Rf；另一函数u＝φ（x）的定义域为Dφ，值域为Rφ.如果Rφ⊂Df，对∀x∈Dφ都有唯一的u∈Rφ⊂Df，从而有唯一的y∈Rf与u相对应，因而对∀x∈Dφ，都有唯一的y∈Rf与之对应.这样就定义了一个由Dφ到Rf的函数，记作
y＝f［φ（x）］，
称此函数是由y＝f（u）与u＝φ（x）复合而成的复合函数，u称为中间变量.
例5 设f（x）＝sin x，φ（x）＝ln x，求f［φ（x）］，φ［f（x）］.
解 （1）因为Df＝（－∞，＋∞），Rφ＝（－∞，＋∞），满足函数复合的条件Rφ⊂Df，所以复合函数为
f［φ（x）］＝sin ln x，
定义域为Dφ＝（0，＋∞）.
（2）因为Dφ＝（0，＋∞），Rf＝［－1，1］，不满足复合条件Rf⊂Dφ，但此时有Dφ∩Rf＝（0，＋∞）∩［－1，1］＝（0，1］，因此复合函数φ［f（x）］＝ln sin x的定义域只能是开区间（2nπ，（2n＋1）π）（n＝0，±1，±2，…）.
注意 并非任何两个函数都可以复合成一个复合函数.例如，f（u）＝arcsin u与u＝x2＋2不能复合成一个复合函数，因为Rφ∩Df＝∅.
求两个函数的复合函数称为函数的复合运算.
例6 设f（x）＝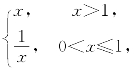
g（x）＝ex，求复合函数f ［g（x）］，g ［f（x）］.
解 函数f（x），g（x）符合函数复合条件，所以有
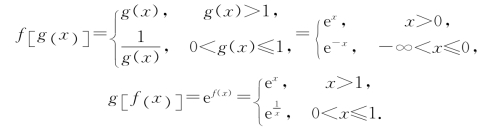
2.反函数
设f（x）的定义域为D，值域为R，由y＝f（x）所确定的x关于y的函数称为已知函数y＝f（x）（直接函数）的反函数，记为x＝f－1（y）或x＝φ（y）.
反函数与直接函数的定义域与值域正好相反，即反函数x＝f－1（y）的定义域为R，值域为D.
注意 这里“反函数”的“反”表示y＝f（x）与x＝f－1（y）的对应法则相反.从几何图形上看，y＝f（x）与x＝f－1（y）的图像在同一坐标系下为同一条曲线.例如，y＝x与其反函数x＝y的图像为同一条直线（Ⅰ，Ⅲ象限的角平分线）.x表示自变量，y表示因变量，所以经常把函数y＝f（x）的反函数x＝f－1（y）记作y＝f－1（x）.因此，直接函数y＝f（x）与其反函数y＝f－1（x）在同一坐标系下的图像就不是同一条曲线了，它们关于直线y＝x对称（见图1－8）.
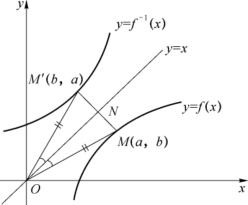
图1－8