培养小学生数形结合的习惯
苏海波
数形结合是数学中四种重要思想方法之一，对于所研究的数的问题，有时可研究其对应图形的性质，帮助理解使问题得以解决（以形助数）；或者对于所研究的图形问题，可借助于对应图形的数量关系使问题得以解决（以数助形），这种解决问题的思想称之为数形结合思想。华罗庚先生曾指出：“数缺性时少直观，形少数时难入微；数形结合百般好，隔裂分家万事非。”那么，数形结合思想方法到底是否像华罗庚先生描述的那般重要呢？
《小学数学课程标准（2012版）》中的内容标准指出：“能运用图形形象地描述问题，利用直观来进行思考。”然而，万丈高楼平地起，我们要想学生将来能够将数形结合思想在数学中运用得得心应手、如鱼得水，我们应该从现在——小学阶段开始充分培养学生的数形结合思想，打好基础。那么，在小学阶段数形结合思想应该从哪几个方面进行渗透呢？下面是我的一些心得与体会：
1．数形结合思想在学习“认数”中的运用。在一年级学生学习认数时，学生对数字没有清晰的概念，但是对于图形或者实物接触得比较多，相对来说要敏感些，这时，可以借助图形或者实物来直观、形象地描述数字，将抽象的数字转化成具体的图形或实物，学生就更容易接受，更能培养学生的数感和理解数字的意义。
2．数形结合思想在学习“十以内的加减法”中的运用。对于一年级的学生来说，思维还处在一个很低的阶段，而且刚接触数学，对数字和算法也很不敏感，在教学时可以采用“以形助数”方法来帮助学生学习、理解。如：
5 + 3 =
△△△△△ △△△
一共是8个△，所以5+3=8，这样可以使学生很直观、形象地理解加法运算就是计算两个数量合在一起是多少，让学生能够很轻松地理解加法运算的算理，使学生更容易达到这一课时的教学目标。
3．数形结合思想在学习“分数”中的运用。在学习《分数的初步认识》这一课时，对于刚接触分数的学生来说，学习、理解起来比较困难，通常采取图形的方法来帮助理解和认识分数，这样学生通过图形的直观描述，就很容易理解，学习起来就很轻松印象也深刻。如：
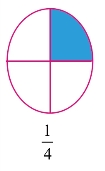
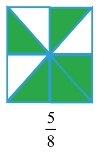
第一个图：把一个圆形平均分成4份，占其中1份，就是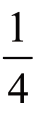
。
第二个图：把一个正方形平均分成8份，占其中5份，就是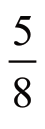
。
这样通过图形帮助理解，可以轻松地让学生认识分数，并能很好地理解分数所表示的意义。
4．数形结合思想在解决“植树问题”方面的应用。学生在解答植树问题时，可以采用线段图来帮助解题，这样可以大大避免出现错误，还可以很直观地通过图形来理解中间的道理。如：
植树节到了，学校组织同学们在全长100米的小路一边植树（两端都栽），每10米一棵。一共需要多少棵树？
通过线段图，我们可以很直观的数出有10个间隔，却有11棵树，学生就很容易知道：棵数=间隔+1。那么，这一题的解就是：100÷10=10，10+1=11（棵）。植树问题的类型比较多，学生常常会把公式弄混淆。我们也可以借助数形结合思想用线段图的方法来帮助他们理解记忆。
5．数形结合思想在解决“行程、工程”问题方面的应用。行程问题和工程问题是小学阶段两个重要的问题，题型比较多、比较杂。学生在遇到一些比较复杂的题型时，常常不知道怎么下手，没有思路。此时，可以借助画线段图来帮助分析思考，从而找到解题的思路。如：
一辆公共汽车从甲地开往乙地，行到中途休息的时候发现行驶了全程的还差20千米，已知剩下的路程是已经行驶路程的5倍，求全程有多少千米？
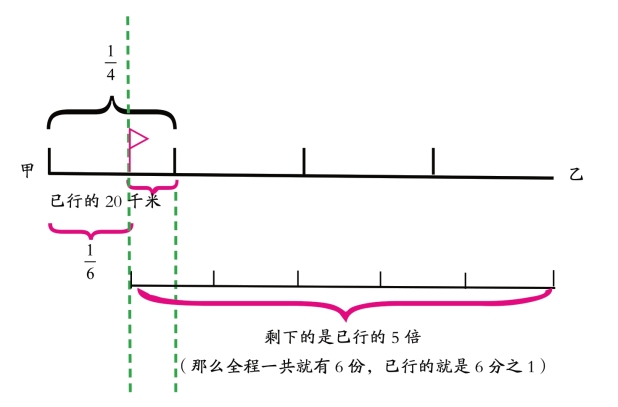
通过线段图，我就可以很直观的分析到，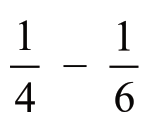
对应的是20千米。那么要求全程就很容易了，
，
。
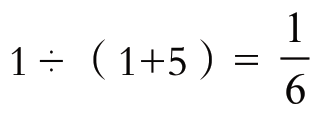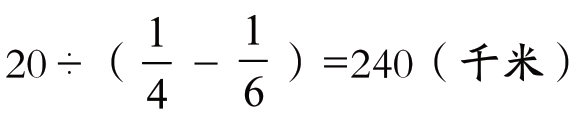以上谈到的是数形结合在小学数学中运用的几个方面，可见，数形结合在小学数学中的重要性，它有利于学生理解和学习新的知识，有利于学生分析题中数量之间的关系，启迪思维，拓宽思路，迅速找到解决问题的方法，从而提高分析问题和解决问题的能力。因而在教学过程中，教师应充分利用“数形结合”优势，引导学生在解题研究中多利用图形来帮助分析、理解，更重要的是培养学生数形结合的思维方式，为以后数学的学习夯实基础。