2.1 数值方法
2026年01月15日
2.1 数值方法
水流运动方程向量形式可写为:

式中:U=(H,Hu,Hv)T;E=(F,G),;
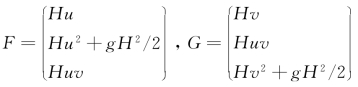
水流运动方程的紊动扩散项E d=(F d,G d),;
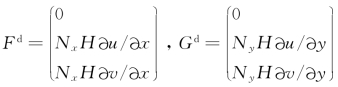 (https://www.daowen.com)
(https://www.daowen.com)
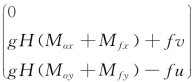
源项M=M 0+M f=,其中H为总水深(m);u、v为流速矢量V沿x、y方向的速度分量(m/s);t为时间(s);f为科氏系数(f=2w sinφ,w是地球自转的角速度,φ是所在地区的纬度);g为重力加速度(m/s2);N x、N y为X、Y向水流紊动黏性系数(m2/s),Mox、Moy为x、y方向的河床底部高程变化;M fx、M fy为x、y方向的底摩擦项。
采用三角形网格对计算区域进行离散,并将单一的网格单元作为控制单元,水深布置在网格顶点,其他物理变量配置在每个单元的中心。将第i号控制元记为Ωi,在Ωi上对向量式的基本方程组(1)进行积分,并利用Green公式将面积分转化为线积分,得
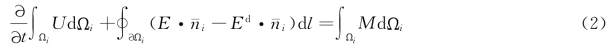
方程(2)求解主要分三部分:一为对流项求解,二为紊动项求解,三为底坡项处理。对流项数值通量可采用Roe格式的近似Riemann解,紊动项采用单元交界面的平均值计算通过该界面紊动黏性项的数值通量,有限体积法底坡项若不加任何处理,则会造成静水的伪流动现象,本文采用“斜底模型”处理底坡项。
