2.1　控制方程

2.1　控制方程

模型采用的水动力三维控制方程如下：

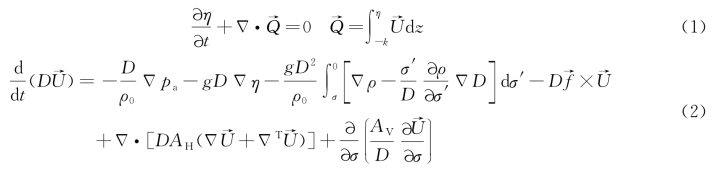
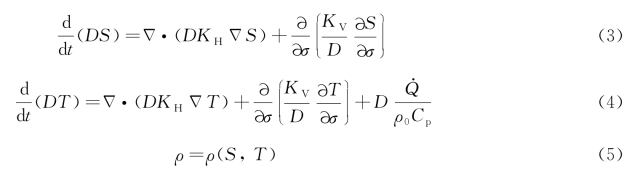
式中：η为自由水面；）为流速矢量；为柯氏力参数；ρ0为参考密度；ρ为水的密度；P a为自由水面的大气压强；A V、A H分别为水平涡黏系数、垂直涡黏系数；S为盐度；T为温度；K H、K V分别为水平扩散系数、垂直扩散系数；Q·为太阳辐射吸收率（W·m－2）；C p为水体比热［J／（kg·K）］；算子。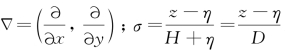

σ坐标系的垂向流速方程为

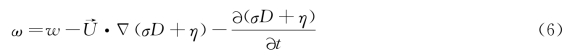
式中：w为z坐标系下的垂向流速。

Smagorinsky亚格湍流模型（1963）得到水平涡黏系数A H和水平扩散系数K H，定义如下：

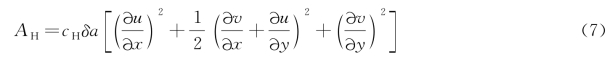
为使上述方程收敛，应给出垂向边界条件。在水面，引入风应力使得动量方程的边界条件收敛：

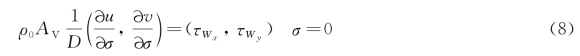
水面风应力由下式得到

式中：ρa为空气密度；CDS为风拖曳系数；W→（x，y）为水面以上10 m处的风速，｜W→｜为其量值，W x、W y为其分量。拖曳系数C DS可由下式计算得出：

当风速量值超出范围时，CDS为一常量。

水底摩阻应力由下式所示：

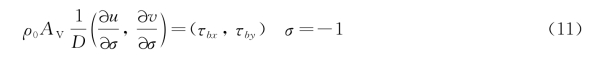
底部应力由下列二次方程给出：

假定边界，且流速呈对数分布，底部拖曳系数CDb可由下式得到：式中：von Karman常数κ＝0.4；z 0＝ks／30，ks为局部底摩阻；δb为底部计算网格的半厚；CDb min通常取值为0.0025。

三维无结构网格变量分配情况如图3所示。另外，紊流模型采用了两个模块，即目前较为流行和成熟的k-kl紊流模型计算模块以及零方程模式，将这两个模块直接引入到本模型中来，不在这里详细累述。

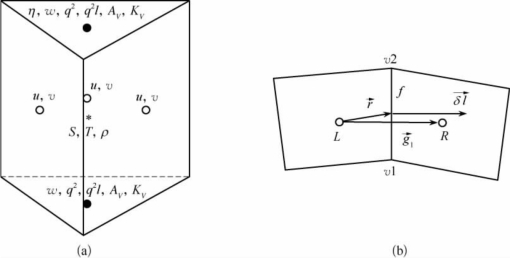
图3　SWEM3D模型的无结构网格变量分配示意图