2.2 基本方程的离散及求解
2026年01月15日
2.2 基本方程的离散及求解
方程(1~4)垂向积分变成二维形式,写成向量形式:

式中:
U=(H,Hu,Hv,HS)T
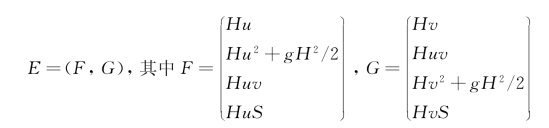
水流运动方程的紊动扩散项:
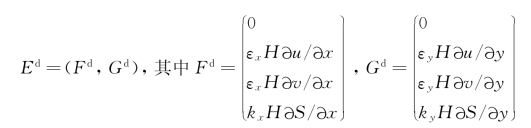 (https://www.daowen.com)
(https://www.daowen.com)
源项M表示为: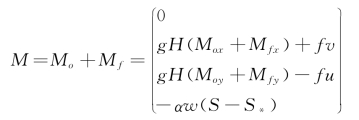
式中:M ox、M oy分别是x、y方向的河床底部高程变化;M fx、M fy分别是x、y方向的底摩擦项;α为泥沙沉降概率;w为泥沙沉降速度;S*为挟沙力。
将第i号控制元记为Ωi,在Ωi上对向量式的基本方程组进行积分,并利用Green公式将面积分化为线积分,得:
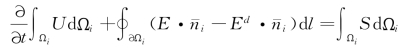
即
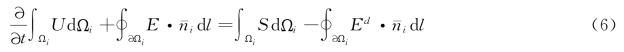
式中:dΩi为面积分微元;d l为线积分微元;n-i=(n ix,n iy)=(cosθ,sinθ),nix,niy分别代表第i号控制元边界单元单位外法向向量x、y方向的分量。方程分为四项:第一项为时变项,第二项为水平对流项,第三项为底坡项,第四项为水平扩散项。
