3.6 波浪场计算方法
SWAN模型采用与WAM模型相同的方程及源汇项，在算法上做了改进并且加入了额外的浅水控制项。SWAN模型对不同水深的适应性较好，且较为全面的考虑了包括能量输入、损耗和非线性相互作用等在内的一系列源汇项；模型以不规则谱型的方向谱表示真实海浪的随机性特征，模拟结果更接近真实海浪。SWAN模型采用动谱平衡方程描述风浪生成及其在近岸区的演化过程。在直角坐标系中，动谱平衡方程可表示为：
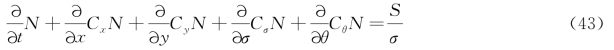
SWAN模型采用全隐式有限差分格式，无条件稳定，允许较大的时间步长。波作用平衡方程离散格式如下：
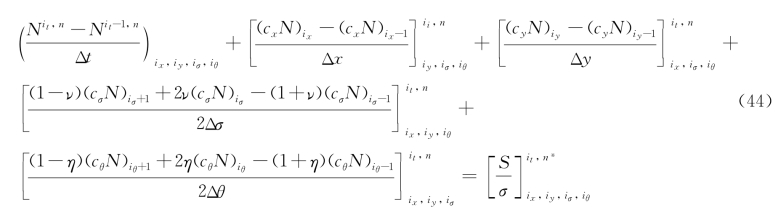
以上两式中：N＝E／σ，为波作用密度变量；i t为时间层标号；i x、i y、iσ、iθ分别为x、y、σ、θ向的网格编号；Δt、Δx、Δy、Δσ、Δθ分别是时间步长、xy坐标空间步长、谱空间相对频率步长、方向分布的步长；ν、η∈［0，1］，两个系数的取值决定了谱空间的差分格式是偏于迎风格式还是中心格式，即决定在谱空间和方向空间的数据离散格式和收敛性强弱。计算时采用一次迭代四次扫描技术。
SWAN模型在对波浪成长的谱型没有任何先验限制的条件下，求解了动谱能量平衡方程。此方程表达了波浪的空间传播、折射变形、浅化效应、风浪生成、能量耗散和非线性波相互作用。
作为第三代浅水海浪模型，SWAN模型可以认为是第三代深水海浪模型的拓展模型。其基本控制方程与原理与WAM模型完全一致，且在深水域使用了相同的源项，包括风能输入、海浪成长、白帽耗散及四波相互作用；而在浅水域中，源项补充了包括底摩阻损耗、三波相互作用和水深引起的破碎等。WAM模型用于海洋尺度的波浪模拟；SWAN模型是模拟从深水到破碎带附近的波浪。WAM模型在空间域和频谱域采用显示差分格式，对浅水海域要求很小的网格尺度，故不适用于近海水域；而SWAN模型采用全隐式差分格式，在浅水海域的模拟中更稳定且节省时间。
SWAN模型的最大优势在于引入最新的源函数公式及计算方法，考虑较为全面且准确，其中风能输入的计算较为完善。
风是海浪的主要驱动因素，但是风—浪作用机理较为复杂，目前为止还没有完善的理论计算公式。在目前关于风能输入的研究中，主要根据Phillips共振理论和Miles切流不稳定理论采用相应的经验公式。
在第三代海浪模型——WAM模型的改进过程中，Janssen等引入的拟线性耦合的气海边界层假定，其考虑了风浪成长过程中海面粗糙度的增加过程。其后，Snyder等为第三代海浪模型引入了Miles—Phillips（切流不稳定—共振）机制使其更加合理。
SWAN模型采用了与WAM模型相同的风能输入形式，其包含线性增长项和指数增长项：
式中：A为Phillips线性增长项；BE为Miles指数增长项。线性增长项在风浪成长初期占主要作用，风浪成长后期主要由指数增长决定。
需要说明的是，SWAN模型输入的为海拔10 m处的风速，而在计算中需要使用摩阻风速U*。参考WAM cycle3（即Komen格式）中，两风速转化关系如下：
CD为拖曳力系数，可以表达为
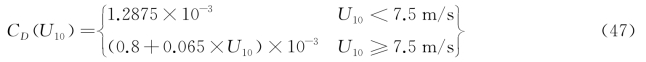
在WAM Cycle4（即Janssen格式）表达形式中，U*的计算过程积分在源项中。
增长系数有很多表达方式，这里只介绍最普遍使用的几种格式。
Phillips线性增长系数，源于Cavaleri、Malanotte-Rizzoli（1981）和Tolman（1992）的研究，其采用一个滤波参数来消除低于Pierson-Moskowitz频率的波浪的成长。
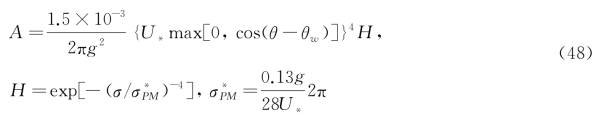
式中：θw为波向；H为滤波参数；
为完全成长海况下的由摩阻风速表达的谱峰频率。
指数增长项有两种可用的表达方式，一种基于Komen的研究，其为U*／c ph的函数。
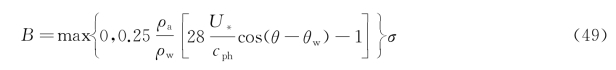
式中：c ph为相位速度；ρa和ρw分别为大气和海水的密度。这种表达方式亦被用于WAM Cycle3。
第二种表达方式基于Janssen的研究，其基于拟线性风浪理论，表达式为：
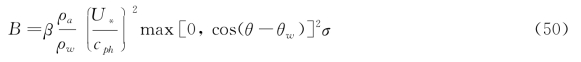
式中：β为Miles常数。根据Janssen的研究，这个参数根据无因次临界高度λ确定。
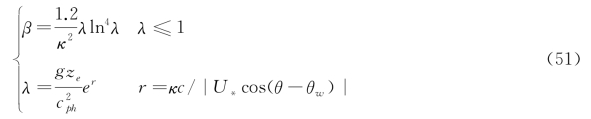
式中：κ＝0.41，为Von Karman常数；ze为有效水面粗糙度参数。如果λ＞1，则β＝0。同时，Janssen假定垂向风剖面为：
式中：U（z）是海拔高度z处的风速；z 0是粗糙长度。有效粗糙长度z e取决于z 0和海况。
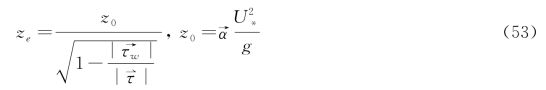
后一方程类似于Charnock关系，其中α→等于0.01。
波应力可以表达为
