2.2　控制方程的离散及计算流程

2.2　控制方程的离散及计算流程

方程离散主要采用时间上半隐式，空间上差分，其中对流项利用欧拉—拉格朗日追踪法求解，具体离散方程如下：

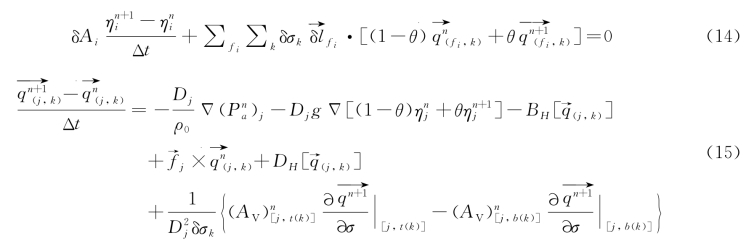
垂向流速一般由连续方程（16）计算得出。

用有限体积法离散上述方程，可得：

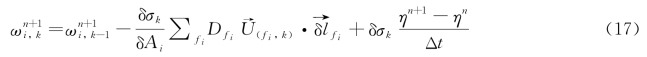
上述方程的边界条件为：

第一步：计算预估流场。

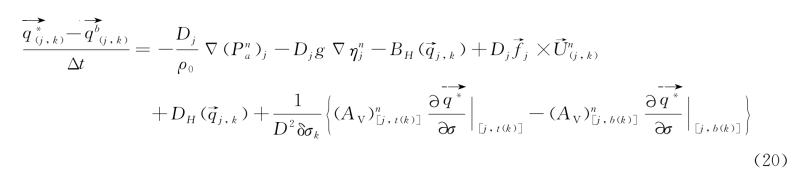
上述方程式可写成：

式中：为三对角矩阵；包含所有的常数项；的定义如下：

代入水面及水底的边界条件，上述方程可以精确求解。

第二步：水位方程隐式计算。

由方程（15～20），可以得到：

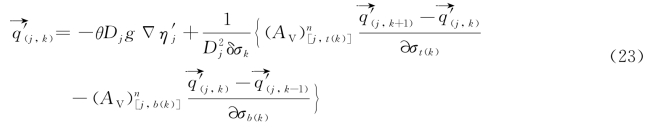
式中。(https://www.daowen.com)

上述方程式可以写成：

式中：为单位矩阵。

方程（14）可以写成：

或者

式中：。

将式（24）代入式（26），可得：

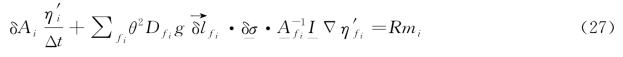
水位余量的梯度可由下式得出：

由此，可以得出下述方程式：

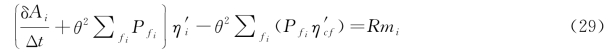
式中：。

显然，上述方程的系数矩阵是对称、正定的，因此可以使用有效的稀疏矩阵。

第三步：水位、流量的更新。