关节型机器人的坐标形式及本体结构
一般工业机器人的本体主要是一只类似于人上肢功能的关节型机械手,它能模仿人的手臂至腰部的基本结构,其系统构成如图7-4-28所示。

图7-4-28 一般工业机器人系统基本构成
当今高性能的关节型机器人中每个关节中均独立设有驱动电动机,通过计算机对驱动单元的功率放大电路进行控制,实现机器人的操作。另外其人机接口还可借助计算机及手持控制器(示教盒)对机器人进行控制和示教操作,从而使机器人具有“示教—再现”功能,表现出通用与灵活的“柔性”特点。
1.关节型机器人的坐标形式
(1)基于基坐标系的机器人分类
1)直角坐标型机器人。直角坐标型机器人是最简单的关节型机器人,如图7-4-29所示,其三个关节皆为主动式移动关节(PPP型),因此有三个自由度,通过三个互相垂直的轴线位移来改变手部的空间位置。直角坐标型机器人易于实现高定位精度,空间轨迹易于求解,但当具有相同的工作空间时,机体所占空间体积是关节型机器人中最大的。
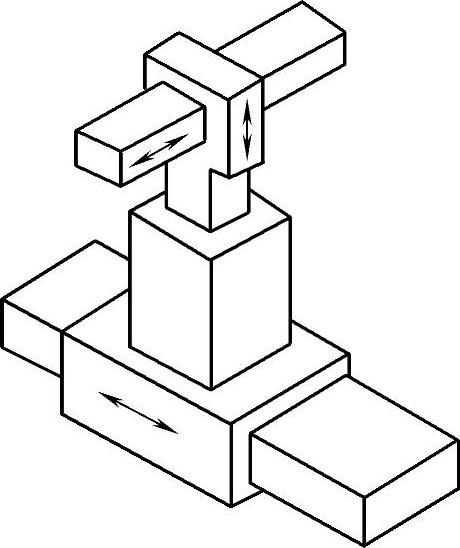
图7-4-29 直角坐标型机器人
2)圆柱坐标型机器人。圆柱坐标型机器人(图7-4-30)有三个自由度,通过两个移动关节一个转动关节(PPR)实现手部空间位置的变化。在相同的工作空间条件下,机体所占空间体积要小于直角坐标型机器人。圆柱坐标型机器人结构简单,便于几何计算,通常用于搬运机器人。
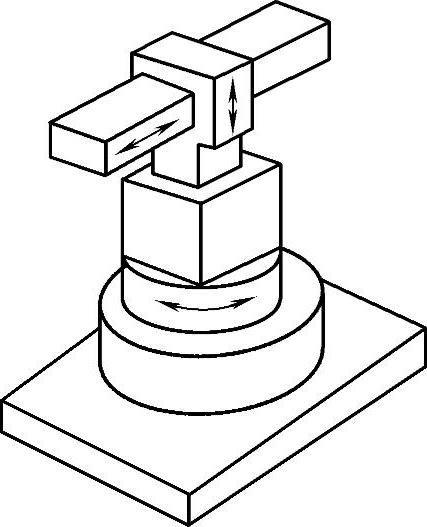
图7-4-30 圆柱坐标型机器人
3)球坐标机器人。球坐标型机器人(图7-4-31)有三个自由度,用两个转动关节和一个移动关节(RRP)改变手部的空间位置。一般是腰关节可绕z轴转动,大臂可在zx平面内俯仰(转动),小臂可伸缩移动。这种机器人的特点是结构紧凑,所占空间体积小于直角坐标型机器人和圆柱坐标型机器人,但仍大于开链连杆式关节型机器人,而且目前应用较少。
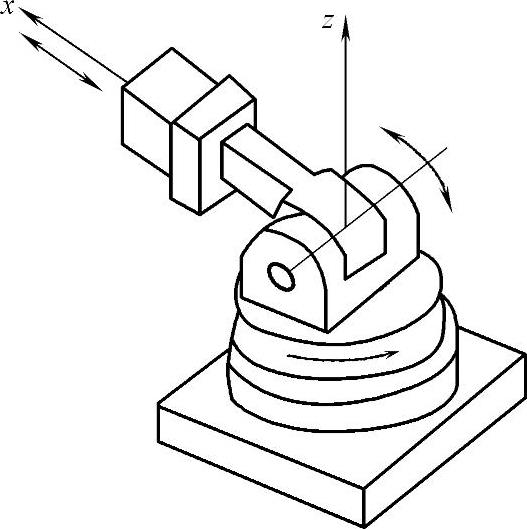
图7-4-31 球坐标型机器人
4)开链连杆式关节型机器人。开链连杆式关节型机器人(以下简称为关节型机器人,见图7-4-32)是模拟人的上臂而构成的。为了保证机器人手部有6个空间自由度,其主动关节数目一般为6,或不少于6。一般情况下,全部关节皆为转动型关节,而且其前三个关节一般都集中在手腕部。关节型机器人的特点是结构紧凑,所占空间体积小,相对的工作空间最大,还能绕过基座周围的一些障碍物,是机器人中使用最多的一种结构形式,世界一些著名机器人都采用这种结构形式。
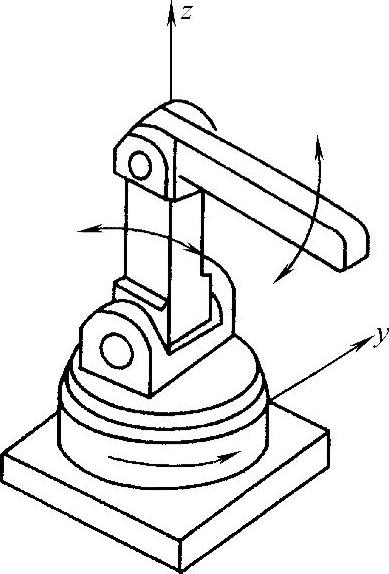
图7-4-32 关节型机器人
(2)关节型机器人的手坐标系和基坐标系
1)关节型机器人手部位姿的概念。在空间中,要确定一个物体的几何状态需要确定其3个位移坐标(或称位置自由度)和3个旋转坐标(或称姿态自由度)。在机器人学术语中,将一个空间物体的上述6个自由度状态称为该物体的位姿。
同理,为了研究机器人的运动与操作,往往不仅要表示空间某个点的位置,而且需要表示物体的方位(Orientation),图7-4-33所示描述了机器人手部的三个姿态自由度——横滚、俯仰和侧摆的概念。
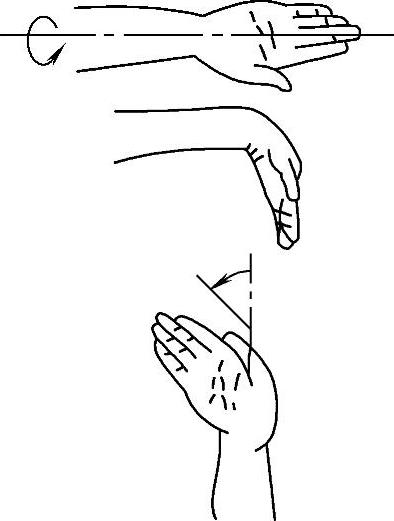
图7-4-33 手部姿态示意图
2)关节型机器人的手坐标系和基坐标系。从运动几何学的角度,可以将多关节非移动型机器人或机械手看成是其一端与基础固接的一系列具有空间运动能力的刚体的连接组合。
通常要在每一个关节上建立运动坐标系,随同关节运动,这些运动坐标系是相对坐标系。关节的转动轴线通常也是运动坐标系的一个坐标轴,坐标的原点一般选在关节转动轴线上的一个便于识别的特征点上,以方便计算。
机器人手部的空间位置和姿态(简称位姿)可以借建立一个固接在手部上的坐标系(通常简称为手坐标系)来描述。手坐标系是相对坐标系,随手部运动移动和旋转。
此外,为操控机器人,还需要将其任何时刻的位姿状态变换到建立在基础上的固定坐标系(通常简称为基坐标系)来描述。基坐标系是绝对坐标系,而且对机器人手部运动的控制也要以基坐标系为参照。
由于手部和基座之间存在着空间距离和方位差别,因此就需要运用一种数学方法,可以方便地将手坐标系所描述的手部位姿转换为由基坐标系进行描述,或是相反。而且,实际上由于机器人上的每一个关节都位于手部和基座之间,其工作状态也必然存在着类似的在不同坐标系之间进行转换的问题。这种数学转换方法被称为齐次坐标变换方法。
齐次坐标变换不仅能够表示机器人的运动学和动力学问题,而且能够表达机器人控制算法、计算机视觉和计算机图形学等问题,有着广泛的应用领域。
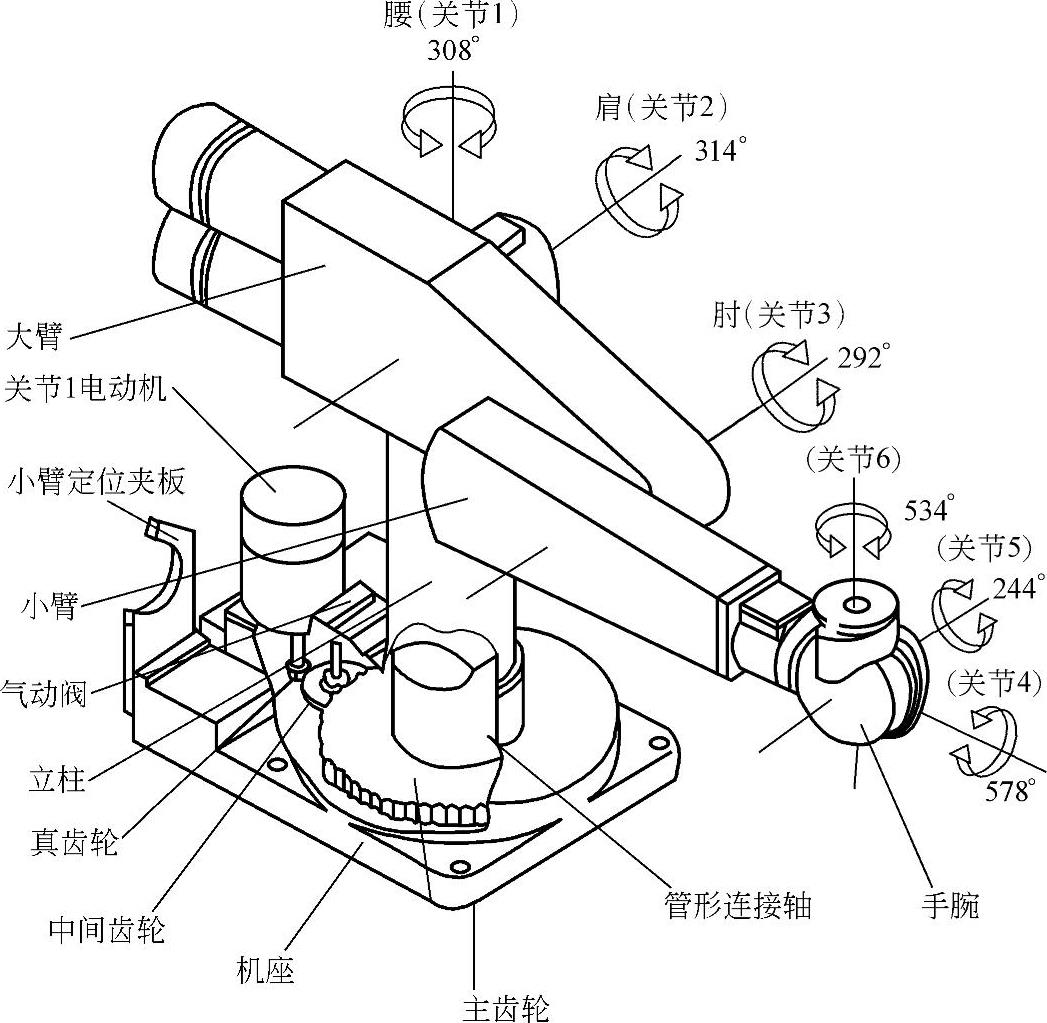
图7-4-34 PUMA—262关节机器人本体结构简图(https://www.daowen.com)
2.关节型机器人本体基本结构
关节型机器人的本体结构是指其基体结构和机械传动系统,通常包括关节型机器人的机座(即底部和腰部的固定支撑)结构及腰部关节转动装置、大臂(即大臂支撑架)结构及大臂关节转动装置、小臂(即小臂支撑架)结构及小臂关节转动装置、手腕(即手腕支撑架)结构及手腕关节转动装置和末端执行器(即手部部分)。图7-4-34给出了此类机器人中的美国优尼美逊(Unimation)公司产的PUMA—262关节型机器人的本体结构简图。
(1)关节型机器人手部转动关节。末端执行器(手部)是关节型机器人直接参与工作的部分。手部可以是各种夹持器,也可以是各种工具,如焊枪、喷头、涂刷等。操作时,往往要求手部不仅能达到指定的位置,而且要有正确的姿态。
组成关节型机器人的连杆和关节,按其功能可分为两类,一类是组成手臂的长连杆,亦称臂杆,产生主运动,是机器人的位置机构;另一类是组成手腕的短连杆,它实际上是一组位于臂杆端部的关节组(图7-4-35),是机器人的执行姿态机构,确定了手部执行器在空间的方向。图示的三自由度手腕能使机器人的手部取得空间任意姿态。
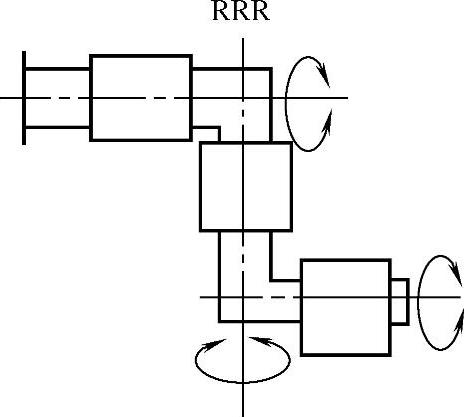
图7-4-35 三自由度手腕关节组
(2)关节型机器人本体的传动系统 该系统包括驱动器和传动机构,它们常和执行机构联成一体,驱动臂杆和夹持的载荷完成指定的任务。常用的驱动器有电动机、液压及气动驱动装置等。其中电动机驱动器最常用,包括直流伺服电动机、交流伺服电动机及步进电动机等。电动机驱动具有精度高,可靠性好,能以较大的变速范围满足机器人应用要求等优点。液压驱动具有输出功率大,惯量小,压力和流量容易控制等优点,常用于负载较大或需要防爆的场合。气动驱动成本较低,易于管理,适用于较简单和负载较轻的机器人上。
1)腰关节驱动器和齿轮传动机构。图7-4-36所示为PUMA—262关节型机器人腰关节(关节1)驱动器和齿轮传动机构简图。
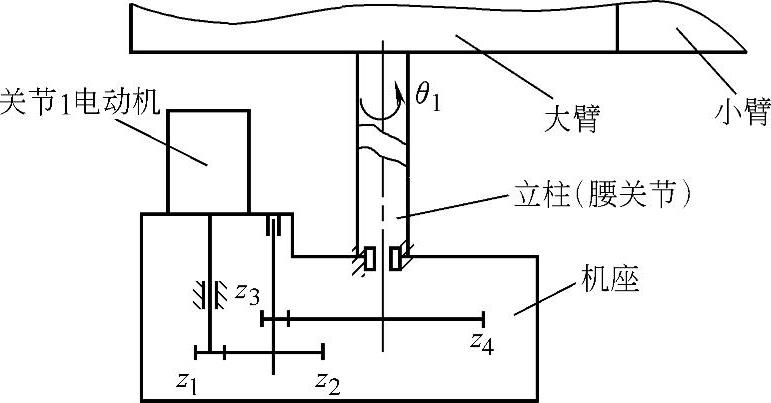
图7-4-36 PUMA—262关节型机器人腰关节 驱动器和齿轮传动机构简图
2)大臂到手腕部的驱动与传动系统。图7-4-37所示为从大臂到手腕部共5个关节的驱动和传动体系简图。
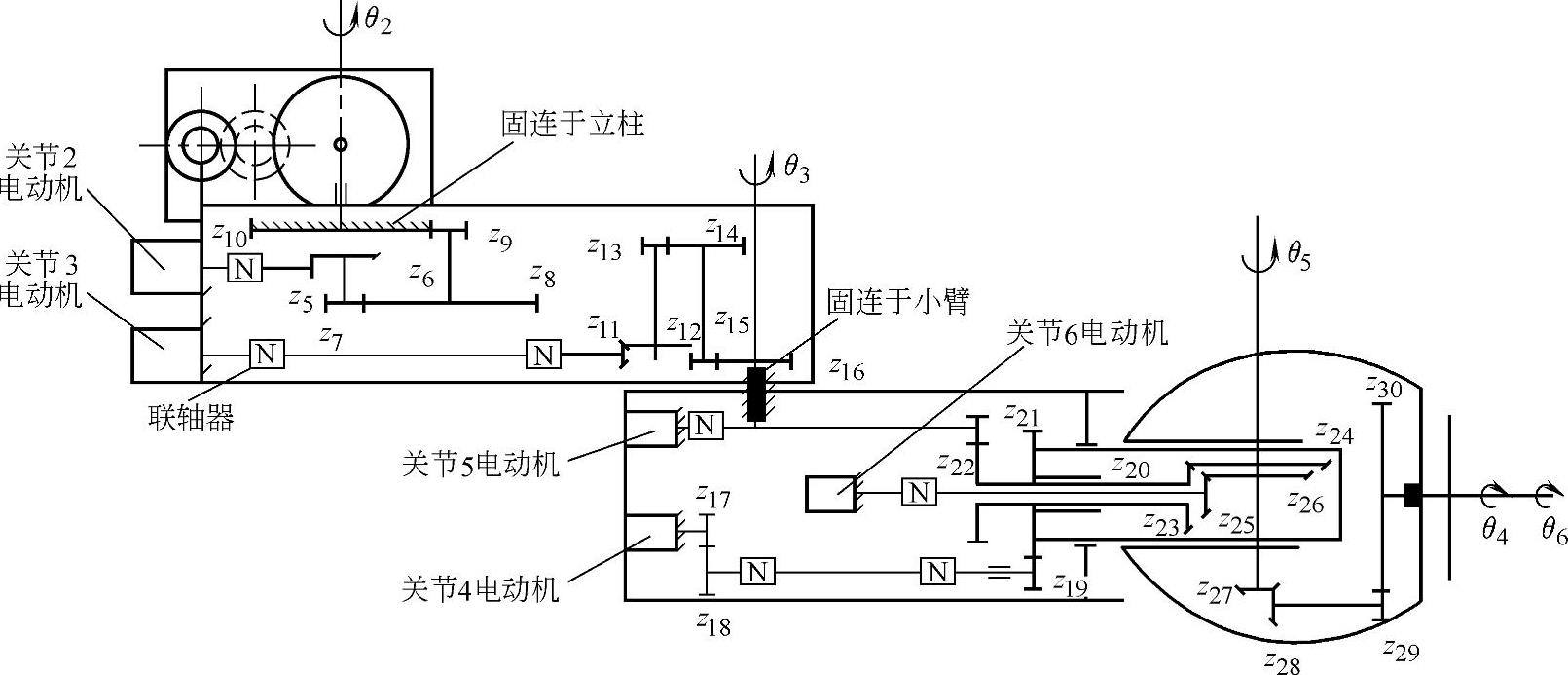
图7-4-37 PUMA—262关节型机器人传动原理图
上二图亦表明,机械传动系统共有30个齿轮,为了实现在同一平面改变传递方向90°,其中有10个齿轮为圆锥齿轮,这样有利于简化系统运动方程式的结构形式,比采用蜗轮蜗杆机构方便。另外,在腕部空间紧凑处,还采用了3层嵌套的空心轴结构,这是多关节腕部的典型结构。
图7-4-38给出了PUMA—262关节型机器人的大臂关节(关节2)和小臂关节(关节3)的传动结构参考图,该图以立体图的形式作为图7-4-37所示传动原理图的补充说明,图7-4-39所示则是表示手腕部3个关节(关节4、5、6)的立体传动参考图。
关节型机器人的本体和其他机器相比,其结构特点为:
1)可以简化成各连杆首尾相接、末端无约束的开式连杆系,连杆系末端是自由而无支撑的,这决定了关节型机器人的结构刚度并不高,并且随连杆系在空间位姿的变化而变化。
2)开式连杆系中的每根连杆都具有独立的驱动器,属于主动连杆系,连杆的运动各自独立,不同连杆的运动之间没有依存关系,运动灵活。
3)连杆驱动扭矩的瞬态过程在时域中的变化是非常复杂的,且和执行件反馈信号有关。连杆的驱动属于伺服控制型,因而对机械传动系统的刚度、间隙和运动精度都有较高的要求。
4)连杆系的受力状态、刚度条件和动态特性都是随位姿的变化而变化的,容易发生振动或出现其他不稳定现象。
由于上述特点知,合理的机器人本体结构应当使其结构系统的工作负载与其自重的比值尽可能大些,结构的静刚度尽可能高些,并应尽量提高系统的固有频率和改善系统的动态特性。
3.关节型机器人的基本参数和特性
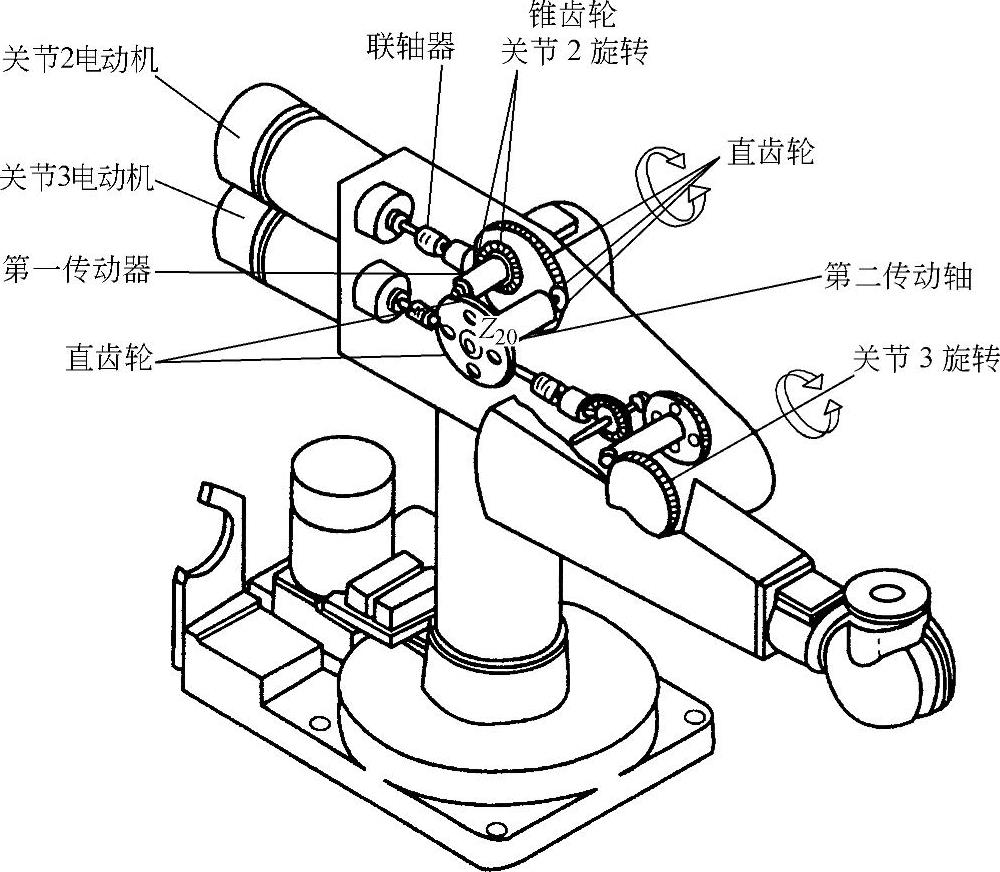
图7-4-38 PUMA—262关节型机器人大小臂关节驱动结构
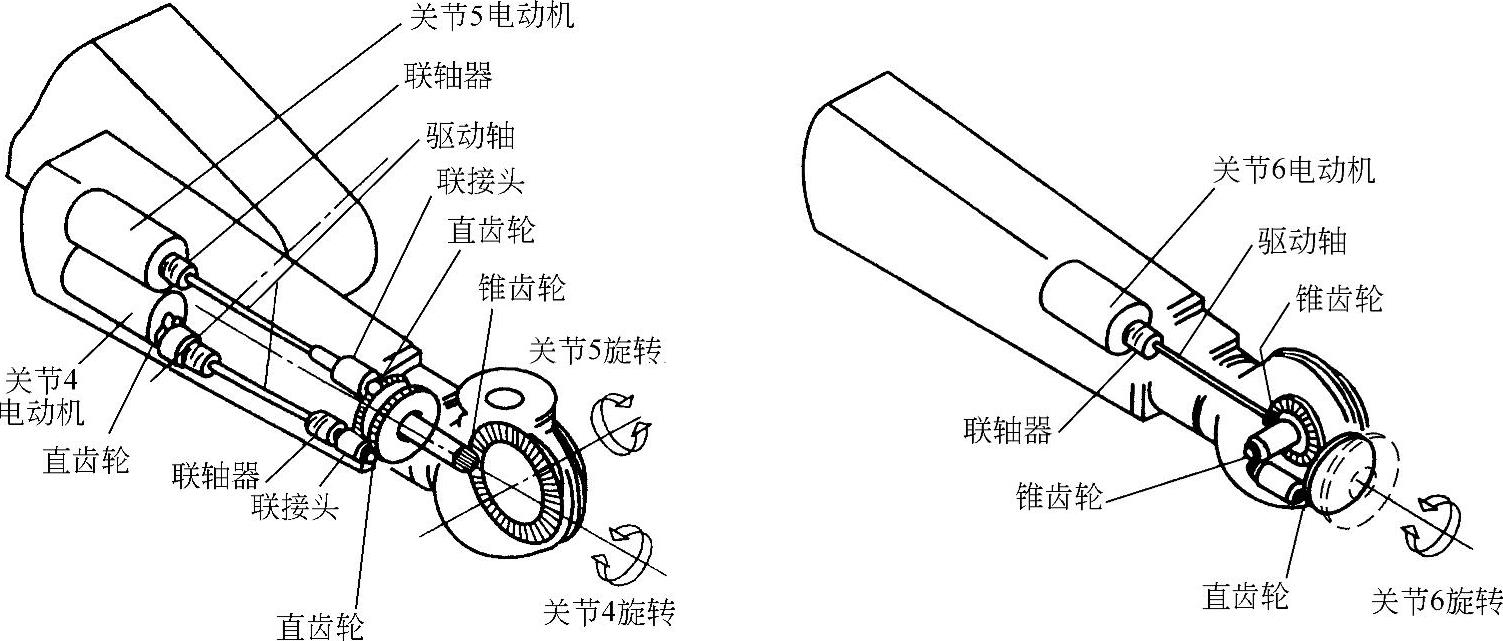
图7-4-39 PUMA—262关节型机器人手腕部3关节驱动结构
(1)工作空间 工作空间是指机器人臂杆的特定部位在一定条件下所能到过空间的位置集合。通常工作空间指的是手腕上机械坐标系的原点在空间能到达的范围,也即手腕端部法兰的中心点(图7-4-34)在空间所能到达的范围。
(2)自由度 机器人为一个开式连杆系,其每个关节运动副仅有一个自由度,故机器人的自由度数就等于它的关节数。目前生产中应用的机器人通常具有4~6个自由度。
(3)有效负载 它表示机器人的负荷能力,即指机器人在工作时臂端可能搬运的物体质量或所能承受的力。机器人的有效负荷能力又可分为额定可搬运质量和有效负载,前者是指其臂杆在工作空间中任意位姿时腕关节端部都能搬运的最大质量,后者则用手腕法兰处的输出扭矩来标示。
(4)运动精度 它主要包括位置精度和重复定位精度。其中位置精度是指机器人臂端定位误差的大小。位置误差除和系统分辨率有关外,还和机械系统的误差有关,尤其是和结构的间隙(如齿轮和齿轮间的间隙、丝杠螺母间隙、液压驱动器间隙等)以及臂杆的变形有关。通常机器人的位置误差为1mm,装配机器人的位置误差要小一些,约为0.1mm或更小。重复位置精度是指手臂端点实际到达点最大分布宽度。机器人臂杆的重复位置精度一般都要高于其位置精度。
(5)速度 速度和加速度是表明机器人运动特性的主要指标。这是因为由于驱动器输出功率的限制,以启动到达最大稳定速度或从最大稳定速度降速到停止,总需要一定时间。对于同样的运动参数,运动路线长则有效速度相对最大稳定速度的差别就小;运动路线短,则有效速度相对于最大稳定速度的差别就会大一些。在机器人实际工作中,短距离的工作点的比例相当大,故在考虑机器人运动特性时,除规定最大稳定速度外,还应注意其最大允许的加减速度。
(6)动态特性 动态特性是机器人机械设计和分析的重要内容。结构动态参数常用质量、惯性矩、刚度、阻尼系数、固有频率和振动模态来表征。在设计时尽量减小质量和惯量,但须提高臂杆的刚度,增加系统的阻尼,提高系统的固有频率。
