从数量研究到模糊集合出现

随着电子计算机、控制论、系统科学的迅速发展，要使计算机能像人脑那样对复杂事物具有识别能力，就必须研究和处理语言的模糊性。1965年，美国加州大学的札德教授Zadeh在《Information and Control》杂志第八期上发表了论文《模糊集合》，文章中引用“隶属函数”的概念，首次成功地运用数学方法描述模糊词项，从而奠定模糊理论的基础。他通过引进模糊集（边界不明显的类）提供了一种分析复杂系统的新方法。他提出用语言变量代替数值变量来描述系统的行为，使人们找到了一种处理不确定性的方法，并给出一种较好的描述人类思维推理的模式。

集合论的重要意义就一个方面，在于它把数学的抽象能力延伸到人类认识过程的深处。一组对象确定一组属性，人们可以通过说明属性来说明概念（内涵），也可以通过指明对象来说明它。符合概念的那些对象的全体叫做这个概念的外延，外延其实就是集合。从这个意义上讲，集合可以表现概念，而集合论中的关系和运算又可以表现判断和推理，一切现实的理论系统都可能纳入集合描述的数学框架。Zadeh（1965，1973）、Goguen（1967，969）、Santos（1970）、Le Faivre（1972）都从不同角度从传统的集合论中发展了模糊集合论，开始以定量技术来处理复杂系统中的有关认知模糊性的问题。

Zadeh等人主要有以下几大贡献：①系统的复杂性增加，人们描述的精确度随之下降，直到达到二者平衡的临界点为止。②在模糊集合中允许语词和数字同时存在，“年龄”可指代非常年轻、相当年轻、年轻、中年、不太老等意义，但它同时可以在系统中与数字一起进行演算。③一种类别往另一种类别的过渡是一种逐渐演变的过程。而不是一次性的突变的结果。④传统的集合论仅是模糊集合论的特例而已。

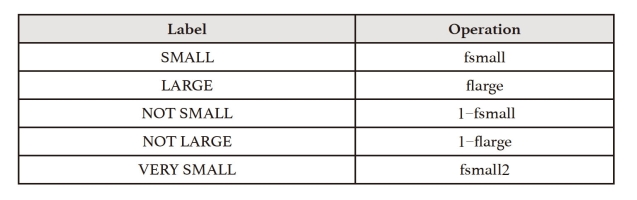
把人类的语言和思维过程提炼成数学模型，才能给计算机输入指令，建立合适的模糊数学模型，这是运用数学方法的关键。Zadeh采用模糊集合理论来建立模糊语言的数学模型，使人类语言数量化、形式化。模糊集合和运算符号（如下表所示）

Table 1　Labels of Fuzzy Sets And Their Predicted Operations

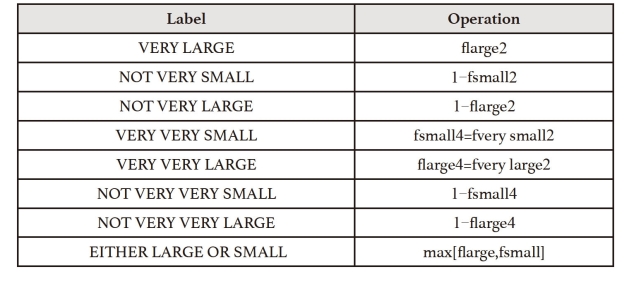
续表

举例来说，“不小”的运算的方式就是将1减去“小”的结果，即公式中的1-famall，结果就是“不小”以此类推，模糊运算同时表达了概念与运算。