DISTORTION MEASURES
Let X=｛x1，x2，…，xT｝be the sequence of test vectors and ck（i），k=1，...，M be codevectors in the ith codebook，i=1，…，N.The task is how to compute the distortion d（xt，i）between xt and the ith codebook.In the simplest way based on the nearest neighbor rule，the distortion d（xt，i）is defined as the distance between vector xt and its nearest codevector in the ith codebook
where the most commonly used measure is the Euclidean distance.In the alternative way proposed in this paper，to minimise the dissimilarity between the vector xt and the ith codebook，the distortion should be the minimum value of the following fuzzy objective function
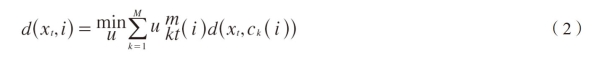
where m＞1 is the degree of fuzziness，ukt（i）is the fuzzy membership associated with the vector xt for the kth class in the ith codebook and satisfies
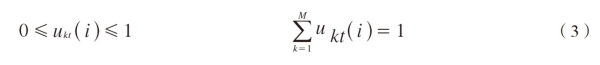
Since the fuzzy objective function is minimised when
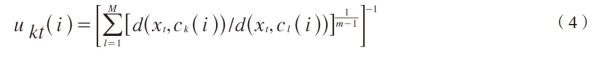
Replacing（4）into（2）gives the minimum value of the fuzzy objective function
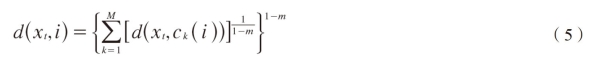
It should be noted that，the expression of d（xt，i）in（5）is very similar to the distance defined in the prototype-based minimum error classifier for speech recognition（McDermott，1994；Katagiri，1998）
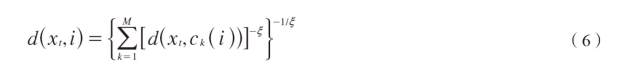
Whereξ＞0，usually constant.Indeed，if we letξ=
since m＞1，we obtain ξ＞0.Therefore，it can be said that a fuzzy set-based interpretation has been found for the distance in（6）.As m is close to 1，it means ξ is large，the distance in（5）can be seen to correspond to the distance in（1）.In other words，the fuzzy k-nearest neighbour rule approaches to the nearest neighbour rule.