The EM algorithm
The purpose of the EM algorithm is to maximise the loglikelihood from observable data.Suppose a measure space Y of unobservable data exists corresponding to a measure space X of incomplete data.For given x ∈ X，y ∈ Y and the parameter model set ʌ，let P（x|ʌ）and P（y|A）be probability density functions defined on X and Y respectively.To maximise the log-likelihood L（x，ʌ）=logP（x|A）of the observable data x over ʌ when y is discrete，the following Q-function is used：
where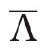 
and A are two parameter sets.The basis of the EM algorithm lies in the fact that if Q（A 
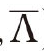）≥Q（A，A）then L（x 
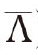）≥L（x，A）.The following EM algorithm is defined as［1］
The EM algorithm：
1.Define y and choose an initial estimate ʌ；
2.E-step：compute Q（ʌ，ʌ）based on the given ʌ；
3.M-step：determine A，for which Q（ʌ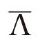
）is maximized；
4.Set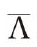 
=A，repeat from step 2 until convergence.
For multiple-prototype classifier design，we consider the case of K models，each consisting of c prototypes.Since the likelihood function is maximised，the decision rule for the EM-based classifier is the following：
Assign x to model k*if
