The fuzzy EM algorithm in the HMM
Discrete HMM：
The family of fuzzy Q-functions is as follows［16］
where
·A=｛π，A，B｝denotes the complete parameter set of the HMM，with π=｛πi｝，1≤i≤N，is the initial state distribution，A=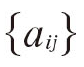
，1≤i，j≤N is the state transition probability distribution，and B=｛bj（k）｝，1≤i≤N，1≤k≤M is the observation symbol probability distribution.
·P（O，S|ʌ）is the joint probability of the observation sequence O=o1，o2，...，oT and the state sequence S=s1，s2，...sT，given the model ʌ
·uS（O）is the membership function，denoting the degree to which the observation sequence O belongs to the state sequence S，and satisfies.
For the E step，to compute（9）is rewritten as
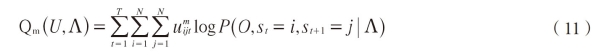
where uijt=uijf（0）is the membership function，denoting the degree to which，the observation sequence 0 belongs to state i at time t and to state j at time t+1，satisfying
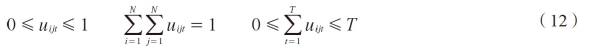
and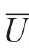 
can be determined as follows
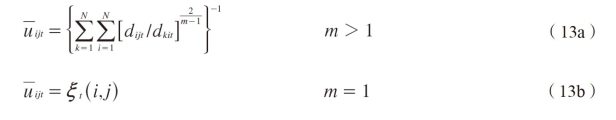
where
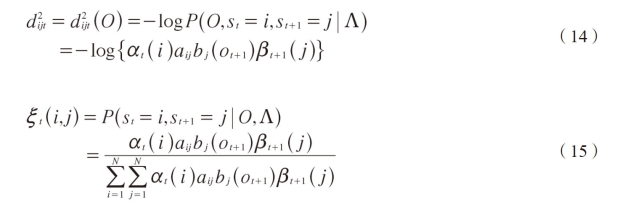
αt（i），βt（j）are the forward and backward variables，respectively.［3］
For the M step，to compute A，using the Lagrange multipliers the parameters of HMMs are reestimated as
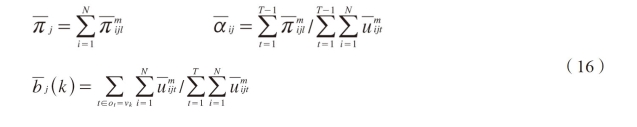
It can be seen that，as m=1 we obtain the Baum-Welch reestimation formulas in the conventional HMM.