A robust clustering approach for the fuzzy EM
Both the EM and the fuzzy EM algorithms have a common disadvantage in the problem of sensitivity to outliers.As seen in(5a)and(5b),the degrees of belonging of a feature vector x across classes always sum to one for both clean data and noisy data.However,it would be more reasonable that,if the feature vector comes from noisy data or outliers,the degrees of belonging should be as small as possible for all classes,namely,the sum should be smaller than one.This property is important since all model parameters as seen in(16),(23),and(29)are computed from these degrees of belonging.In(20),Dave proposed the idea of a noise cluster to deal with noisy data or outliers for fuzzy clustering methods.It was shown in[23]that this approach is quite successful in improving the robustness of a variety of fuzzy clustering algorithms.Consequently,this approach can be appjied to the FHMMs and the FGMM.The major advantage of this approach is that it is a robustified version of the FHMMs and the FGMM and it can be uscd as alternative towards the FHMMs and the FGMM.Our approach here is regarded as the noise clustering(NC)method,the noise is considered to be a scparate class and is represented by a prototype that has a constant distance,δ from all feature vectors.The membership u.(x)of the obscrvable data x in the noise unobservable data(classes or states)is defined to be

Therefore,the membership constraint for the"good'l classes or states is effectively relaxed to

This allows noisy data and outliers to have arbitrarily small membership values in good classes or states.The fuzzy objective function in the NC approach is as follows
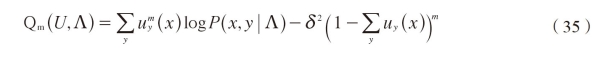
and the following membership can be derived by
diffcrentiating(35)with respect to uy(x)
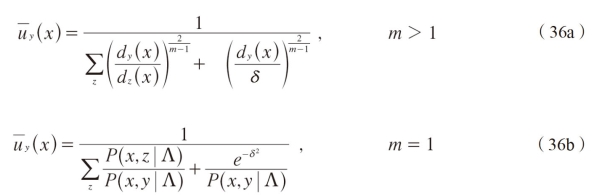
Based on Dave's idea,we obtain the following for m=1.
Comparing with(5a)and(5b),we can see that the sccond terms in the denominators of(36a)and(36b)become quite large for outliers,resulting in small membership values in all the good classes or states for outliers.This modification has been applicd to FHMM[21]and FGMM[22]for speech and speaker recognition.
