句子结构及篇章之间的数理描写
把句子及整个篇章形式化，这是应用语言学等许多学科极为需要的。而这种结构的逻辑化，只能从自然语言中得来。从逻辑学角度讲，语言的定义是什么呢？沙夫是这样定义它的：“这些语词指号是用来主观认识反映客观实在的过程中表述思想，并且用来社会地交流这些关于实在的思想，同样地用来交流有关的感情的、美感的、意志的等等的经验。”语言是一种特殊的严格的符号体系，它具有指谓性与交际性，因而它能够被描写。传统语法关于歧义句的分辨，以及层次分析法的进行，都是以语义逻辑为基础的。
我们来描写下面一些句子：
先看一首民歌：“樱桃好吃树难栽，山歌好唱口难开；要吃樱桃先栽树，耍唱山歌拉下脸来。”数理逻辑的分析是：
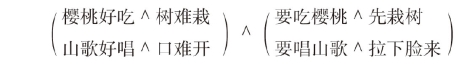
这是一首与七言诗韵律相符的民歌，前两行可用意合取法，是合取的合取，格式可代为：（P∧P）∧（r∧S）
后两行的四个小分句依次与前四个相似，用P'、q'、r'、S'代，其中S'代“拉下脸来”与“开口”是不同的命题，但它们是充要条件关系。即，拉下脸来，就开得了口；拉不下脸来，就开不了口。全首的逻辑关系是后半首对前半首的进一步说明，前半首只是两两平列四件事（P、q、r、S），后半首进一步说明它们之间的条件关系。因而在逻辑上全属合取关系。全首逻辑结构为：
只要将变元代入，我们就可得到全首诗。
下面再看一个复句的分析：
“人不犯我，我不犯人，人若犯我，我必犯人。”其逻辑格式是：
公式极其简明。
我们知道数理逻辑是以其推论完整性及严密性而逐渐在取代着形式逻辑的地位的，其所有的符号极其简单，表示各种语言单位之间（甚至句子）之间的关系符号只不过五个，有的人甚至只用三个，但是通过一系列的符号运算，就可以对语言中所有的逻辑结构进行描述。这五个符号就是合取∧、析取V、否定
、蕴涵→，等值↔，只要通过谓词演算系统，其之间各种关系便会暴露无遗，从而使应用语言学得以迅速发展起来。
我们再举一例：“谁爱说什么，就说什么。”（老舍）这里分析得到：有两个个体变项x，y，可以用φ代表人，即“谁”，用y代表“什么”，ψ代表“爱说”，x代表“说”。这个复合命题便表达为：
同时数理逻辑也引入了集合论的运算规则，如德摩根律，双否律，蕴析律等等，使得它在计算机的运算成为可能。只要我们编出程序，句子便可以产生。
综上所述，数学已开始应用于语言学的研究，从语言的定义到作家的风格比较，从共时语言学到历史语言学，都可以得到数学上的构拟。但目前最大的问题在于：必须经过大量的调查，找出可靠的数据来。