语法的数学模型
汉语、英语等语言的主要语法手段是词序，词序决定了某一词类的语法功能，具有这一语法功能的词类实际上是具有某一共同元素的功能集合，传统语法的主语、宾语等概念便因此而产生。这种例子无须多举。但是它因为是对单个句子进行分析，很难体现出语言单位之间的那种既联系又对立的依存关系。语法的数学模型应该是这样的：一切语法现象都应该体现在排列组合之中，一切的问题都应该在这种关系中去寻找。道理是也很简单，语法无非是组合关系。例如词语搭配的不合逻辑性、不合语法性，只须变更一个次序就可，而这一不合语言要求的原因，又是由于类属的搭配不当，这样一来，我们便可找到症结所在。同样，语言的几个特征，一样可从数学上加以说明。假设某一语法系统具有m个层次（音素构成到组句成篇章），而每一层次又具有m个元素，那么期排列组成的总的可能单位有
=Mm个，这是一个巨大的天文数字，可是在如此巨大的数目之中，仅有极少部分成为语言的东西。以单个词构成的句子为例，有人统计过，英语中仅由三十个以下的词可以构成句子的点数为1030，所以在如此浩大的数目中确只有一小部分为人们所用，这无疑体现了语言的任意性原则，但是语言中的同音词、同义词、近义词的存在，又说明了语言的不任意性的原则。在以这一部分符号中，任其滋生，反复使用。有人做过统计，汉语中Si音多达三十多个，这就是不任意性的体现。
我们知道，转换生成语法关于语言的生成性原则是基于数学上的递归理论，在计算机科学上，这种用数学上的严格描写形式为语言应用于计算机科学提供了理论基础。传统语法学对此是无能为力的。它既不能说明其真正的本质，更不能对语言进行描写。而将其归于心理上或其他的原因。我们认为，“属于同一句型”的这一说法过于简单，而应该写出某一句子的一步步生成的过程。我们用一个程序来说明：设S1和S2是两个语法句，S1和S2不同的地方仅在于x出现于S1，而y出现于S2（也就是说，S1=...x...，S2=...y...）而x，y分别在S1与S2中是同类型的成份，这时候要是我们用x+and+y去代替S1里的x，其结果就形成了S3这个新句子（即S3=...x+and+...y...）。一个新句产生过程是这样。同样，反复地使用同一语法结构，我们便可得到许多同类的句子，包括传统语法书中的所有句型。很清楚，社会交际是择其一部分符号但却反复使用。
以上所谈的是语言的音位系统、语法系统组成的一般规则，下面我们来分析一下这些系统又是如何地体现着语法关系的。
假设A1A2A3A4A5A6分别代表六个词i，其排列次序从左到右，且下标数目依次增大。这样我们就可以得到一个句子，它可以是“我给他一本书。” 这类句子（在这里我们权且认为，A1A2...A6分别代表的就是六个词）。
又如如果我们调换一下排列次序：A1A2...A6→A3A2A1A4A5A6那么句子是“他给我一本书”还可再换成“A3A4A5A6A2A1，即：他一本书给我”。乔姆斯基的转换生成语法（Transnational Grammar），基本思想就是这样，只不过多了一些转换规则及制约规定。这样，它体现了语言的经济性原则，用较少的单位去表达较大的概念数目。树形图就是应用的方法：
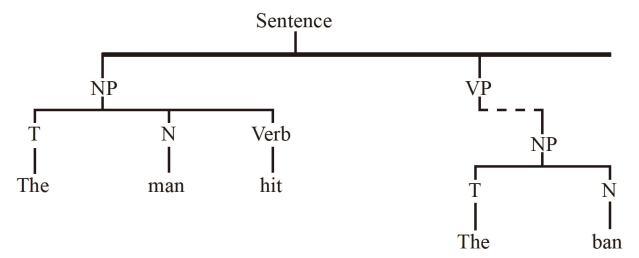
其生成过程如下：
NP+VP （ⅰ）
T+N+VP （ⅱ）
T+N+Verb+NP （ⅲ）
the+N+Verb+NP （ⅳ）
the+man+Verb+NP （ⅴ）
the+man+hit+NP （ⅵ）
the+man+hit+N+N （ⅱ）
the+man+hit+the+N （ⅳ）
the+man+hit+the+ball （ⅴ）
这种分析法已被计算机采用了，其方法依然在集合的范围内：
S1=｛x|x=NP1，NP2...，NPm｝
S2=｛x|x=Verb1Verb2...Verbm｝
这些NP及Verb的各种单位都是在出现在上述树形图范围内。在各自的位置上，很清楚，索绪尔在《普通语言学教程》里提到的将语法纳入横组关系与纵聚关系这一范围内说法在此得到了体现。排列与组合就是索绪尔这一思想的支柱。