2.5 探索思路
1980年李文林、袁向东[2]研究指出,汉代计算上元积年,需要解一到两个相当简单的一次同余式或者一次不定方程。
例如,三统要求历元起于冬至、朔旦、甲子日夜半,同时日月五星齐会。年月日最小公倍数叫统法,一统1539岁,年月日与六十甲子的最小公倍数叫元法。三统为一元,4617岁,太初元年前十一月甲子、朔旦、冬至会合。假设从三统历元到太初元年的积年数为N,应是4617的倍数,记作p,即
N=4617×p(p为整数)。
这样算出的积年,表明三统上元时,日月和岁星都处于起始位置。
李文林、袁向东指出,汉历上元积年推算恰好符合可解性条件,这应该说不是偶然的。汉代历算家利用了太初元年的特殊数据,只需要处理一个同余式。为了改进历法,后世的计算法变得越来越复杂。
公元3世纪魏晋时代,随着天文实测精度的提高,要解两个以上的一次同余式。魏景初历规定以冬至、朔旦与甲子日零时会合之时为历元。
设a是一回归年日数,b是一朔望月日数,近期编历岁冬至距甲子日零时是R1日,离平朔时刻是R2日,那么,景初历上元积年数N就是一次同余式组
a N≡R1(mod 60)≡R2(mod b)
的解。
按历元的定义,从上元到近期编历岁,恰好经过N个回归年,合a×N日。由甲子记日,就是以甲子为首60日为一个周期,所以60去除a N,余数应该是近期编历岁冬至离最近一个甲子日的日数,于是有第一个同余式:a N≡R1(mod 60)。同样的道理可推出第二个同余式,用朔望月日数b去除a N,余数应该是近期编历岁冬至离最近一个平朔时刻的日数,于是有a N≡R2(mod b)。见示意图2.2。(https://www.daowen.com)
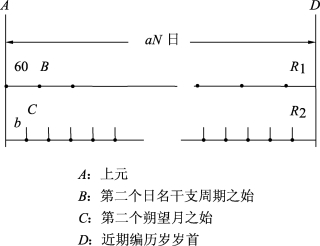
图2.2 历法一次同余式组示意图
三世纪之后,天文观察技术更为精确,刺激着更复杂的一次不定方程或一次同余式,导致历算家努力寻找它们的一般性解法。
由此,我们可以判断,尽管汉代的历算家不一定能掌握处理它们的一般性理论和方法,但至迟到西汉末年,汉代的历算家就有了处理的办法。
从此,中国历史上90多家历法中,有80多家历法将上元积年数据列为历法第一条。从某种程度上讲,一部中国古代的历法史几乎就是上元积年的演算史[3]。
历法是皇权的象征,在中国封建社会中享有至高无上的地位。从刘歆直到元代郭守敬以前,历家往往把毕生心血倾注在上元积年的推算上,埋头于各种天文周期的测验。
到了南北朝(420—589),祖冲之的大明历(公元462年)更要求历元必须同时为甲子年的开始,而且日月合璧,五星连珠,月亮又恰好行经其近地点和升交点。这样的条件下,推算上元积年,就相当于要解十个同余式了。当然,祖冲之很可能要利用一些特殊的数据来消去其中的一部分,不一定就是解十个同余式。
数学家们肯定知道其一般性过程,但未必透彻了解其中的内部逻辑关系,未必能清晰地解释并真正地掌握它。然而,上元积年计算的进一步需要,势必刺激对一次同余式问题的详尽研究,也派生出《孙子算经》的物不知数问题。
钱宝琮[4]指出:“《孙子算经》里物不知数问题的解法不是作者的向壁虚造,而很可能是依据当代天文学家的上元积年算法写出来的。”
总的一句话,古代天文历法中数学计算的需要,确实刺激着一次同余式问题的研究。
