14.4.3 古历会积原题
至此,我们把古历会积题原题原答和原术,照录如下:
古历会积
问古历,冬至以三百六十五日四分日之一,朔策以二十九日九百四十分日之四百九十九,甲子六十日,各为一周。假令至淳祐丙午十一月丙辰朔初五日庚申冬至,初九日甲子。欲求古历气朔甲子一会,积年积月积日,及历过未至年数各几何?
答曰:一会积,一万八千二百四十年,二十二万五千六百月,六百六十六万二千一百六十日。历过,九千一百六十三年,未至,九千七十七年。
术曰:[同前]置问数[有分者通之,互乘之,得通数]。求总等,不约一位,约众位,得各元法。连环求等,约奇弗约偶,各得定母[本题欲求一会,不复乘偶],以定相乘为衍母,定除母得衍数,满定去衍,得奇,以大衍入之,得乘率,以乘衍数,得泛用数,并诸泛以课衍母,如泛内多倍数者损之。乃验元数奇偶同类处,各损半倍[或三处同类者,三约衍母,损泛],各得正用。然后推气朔不及或所过甲子日数,乘正用,加减之,为总。满衍去之,余为所求历过率。实如纪元法而一,为历过。以气元法除衍母,得一会积年,以气周日刻乘一会积年,得一会积日,以朔元法除衍母,得一会积月数。
右本题问气朔甲子相距日数,系开禧历推到,或甲子日在气朔之间及非十一月前后者,其总数必满母,赘去之,所得历过年数,尾位虽伦,首位必异。今设问以明大衍之理,初不计其前多后少之历过。
此题及计算,并不符合一次同余式组。依照“实如纪元法而一”的纪周法,“借用”现代一次同余式组的形式,题问为
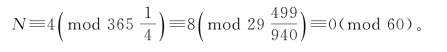 (https://www.daowen.com)
(https://www.daowen.com)
计算过程相当漫长,如置问数、求总等,各得定母、衍母、衍数,得奇、泛用数,得正用数。直到为总,满衍去之,余为所求历过率。误调用数,只是数据巧合,不至于危及全题。
中世纪的一道综合题,一环套一环。前面一步演算有误,即使推算数理无误,也肯定会在后续操作中带来的结果与最初数据不符。数理认识还未透彻,思考还不周到,计算并不正确,本来就不宜苛求于古人,特别不宜于苛求一次同余式领域内的先驱。若据此而判秦九韶满盘皆输,恐怕失之偏颇。
有时,我们只能以前面错误数据为依据,考察当前一步的知识点。通过探求有无导致新的错误,来判定当前知识点是否有误。
整个解题过程,用表格表示(表14.7):
表14.7 古历会积题演算
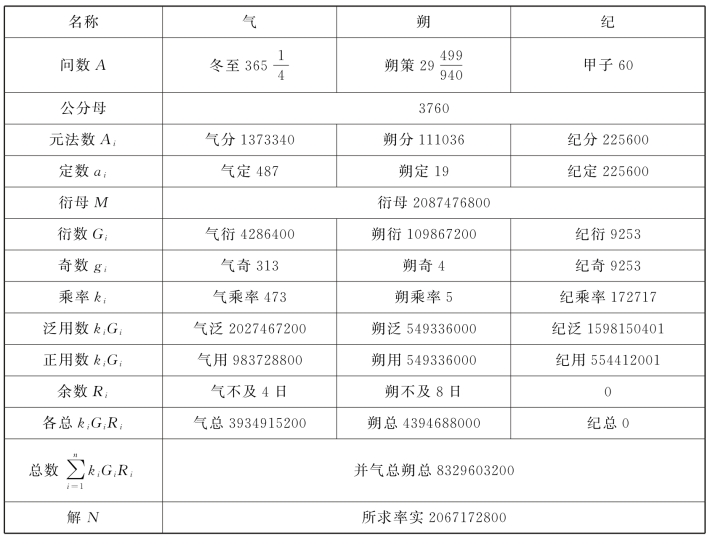
古历会积题众多失误,最重要的失误在于以纪周法立式,替代开禧历的岁周法。
