18.3.1 序列值解法
2026年01月14日
18.3.1 序列值解法
根据《算术研究》第27节,用序列值解法处理137和60,求出不定方程137x+1=60y的一组特殊解x=7,y=16。再用137x+10=60y的一组特殊解。
高斯表述解的依赖性时,采用同余式:
观察形如ax+t≡u的同余式,这个同余式是依赖于ax≡±1的。
而同余式与不定方程等价:
不定方程ax=by±1与以b为模的同余式ax≡+1等价。
分三步解出阿耶波多不定方程:
(1)取137x+10=60y的两系数137和60,计算序列值(表18.2)。
表18.2 偶序整数对137与60序列值计算
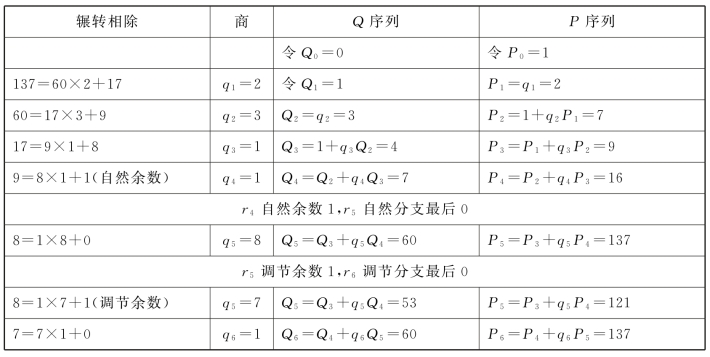 (https://www.daowen.com)
(https://www.daowen.com)
(2)两系数组成的整数对,因自然余数除法序数的奇、偶,分成两大类:奇序整数对和偶序整数对。每大类整数对又因商数损一调节举措,分两个余数分支,组合成四种并列的情况。高斯配置法则说:
当[α,β,γ,…,μ,n]项的个数是偶数时,我们有ax=by+1,当项的个数是奇数时,我们有ax=by-1。
因自然余数1的除法序数4为偶数,项的个数即商的总个数5为奇数,所以选取不定方程137x=60y-1,即137x+1=60y。
因自然余数1序列值是Q4=7,P4=16,所以x=7,y=16是常数1不定方程137x+1=60y的最小正整数解。核算:7×137=959=16×60-1。
(3)不定方程137x+10=60y的常数10是137x+1=60y常数1的10倍。
以x=7,y=16乘10,得x=70,y=160。
再各除以对方系数,得x=70÷60余10,y=160÷137余23,所以x=10,y=23是137x=60y-10的一组最小正整数解。核算:137×10=1370=23×60-10。
可见,x=10,y=23是不定方程137x+10=60y的一组特殊解。
