14.9.2 拼题的破绽
两个独立的追逐问题，合并条件与提问如下：
问有急足三名，甲日行三百里，乙日行二百五十里，丙日行二百里。先差丙往他处下文字，既两日，又有文字遣乙追付，已半日，复有文字续令甲赶付乙。……先欲知乙果及丙、甲果及乙得日并里。
图14.3 程行相及题示意图
甲追上乙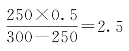
日，甲行2.5×300=750里，称作乙率。
乙追上丙
日，乙行8×250=2000里，称作丙率。
再增添条件和提问，组成全题：
三人偶不相及，乃同时俱至彼所。……次欲知彼处去此里数各几何。
套用大衍术格式，依次计算如下。求定计算的错误，造成后续混乱。
第一步，误算定数。
把三名急足300，250，200作问数，列出化约过程：
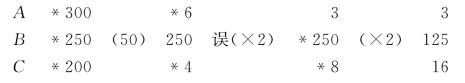
正确的定数应该为3，125和8。定数乘积衍母3000。秦九韶因三数有总等50，就把下一步6和4的最大公约数2，误认作续等。续等复乘，产生了4×2=8。最终成了3，125和16。后面所有数据，如衍母6000，也就跟着错。
第二步，大衍计算。
“各定约衍母得衍数（算草）”，求得甲2000，乙48，丙375。
“求奇数（算草）”，求得甲2，乙48，丙7。
“各以大衍（算草）”，求得甲2，乙112，丙7，“各为乘率”。
“以乘率对乘衍数（算草）”，得甲4000，乙5376和丙2625，称泛用数。
“并三泛，得一万二千〇〇一，乃多衍母一倍，当半衍母六千得三千（算草）。”3000是衍母6000之半，消甲4000，余1000。又消乙5376，余2376。丙2625不消。各为定用数。
“视甲及乙里为乙率，见乙及丙里为丙率，以乙日行满去乙率，不满为乙余，以丙日行满去丙率，不满为丙余（术文）。”
甲行2.5×300=750里，是甲及乙所行里，称作乙率，与乙日行250并没有关系。乙行8×250=2000里，是乙及丙所行里，称作丙率，与丙日行200也没有关系。由此所处的乙余与丙余，两个0都没有意义。
第三步，求解无门。
“以二余各乘本用，并之为总，满衍去之。不满，为彼去此里（术文）。”两个0所乘本用，得各总0，并得总数0。满衍3000去之，不满为0。称“为彼去此里”，显然不宜。
很容易看出，秦九韶编造题目时，预定了答数三千里。3000里是甲乙丙三人“日行”300，250和200的最小公倍数。
算草结尾，秦九韶增添一句：
今乙丙二人所行，各皆适满，去之为无余。虽称同时俱至，乃各系全日所行，便以乙丙二人约六千里，得三千里，为彼去此里数。合问。
秦九韶承认这种适满与无余，改以“同时俱至，乃各系全日所行”为由，搪塞成衍母6000除以2人，得3000里，“为彼去此里数”。
我们只能说：此说反而暴露了题问中“三人……乃同时俱至彼所”的矛盾。
丙日行200里，行3000里，需要15天。
乙日行250里，行3000里，需要12天。乙于第3日卯初出发，行总行程3000里，只需12天，在第15日卯初，到达图中标“乙止”处。乙离3000里处，还要250里。
甲日行300里，第3日中午出发，行总行程3000里，只需10天，在第13日中午，到达图中标“甲止”处。甲离3000里处，还要750里。
因此，题问中“三人偶不相及”是事实，而“乃同时俱至彼所”永远做不到。见图14.3程行相及题示意图。