6.2　求解入手式

6.2　求解入手式

高斯指出：“现在我们考虑不定方程ax=by±1，a，b是正数，不妨假定a不小于b。”我们将称大系数项ax约定。大系数a置于未知数x之前，以保证首次除法的商不会是0。

限定单一不定方程首项为正，a，b为正整数，共有ak±bj=±1的4种形式，小系数和常数1各有一组相反数。相应地，单一同余式ak≡±l（mod±b）也有4种形式，模和常数1各有一组相反数。

8种单一式，加以编号，列表如下：

表6.1　8种单一式

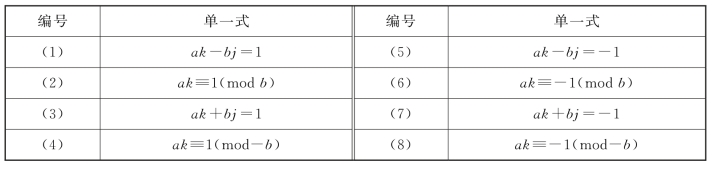
单一式解法可以多种多样，如同余类解法、欧拉函数解法、序列解法和大衍求一术等。

求出特解后，再利用下面所称的解依赖和解转换，可得到其他7种单一式的特解。

现代教科书极其重视解题思维的循序渐进。

奥尔德斯的《连分数》[1]首推形式（1），作入手求解形式：

我们的求解是逐步达到的，通过一些容易的阶梯，最后达到熟练解任何可解的形式如ax+by=c的[不定]方程式的目的。我们首先学会解[不定]方程式ax-by=1，（a，b）=1，这里a和b是正整数。

约定入手求解单一不定方程

ak-bj=1

的一组特解记为x0，y0，它的一切解就是

k=x0+bt,j=y0+at,t=0,±1,±2,±3,…。