17.1.3 闰周的改革
东汉以来的天文观察日趋精密,第一个冲破19年7闰这条锁链的是南北朝时期北凉的赵匪欠,在玄始历(412年)中,他提出了600年间置入221个闰月的新闰周。
下面表17.2“早期若干闰周表”中,摘录早期几个闰周值。
表17.2 早期若干闰周表
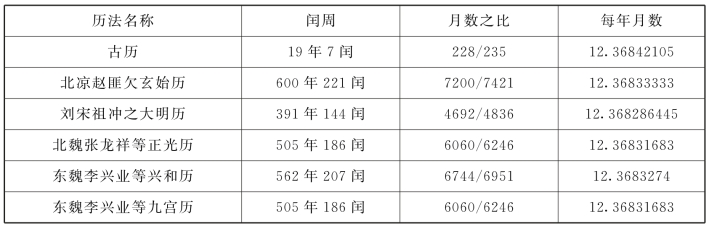
我们用600×12=7200,7200+221=7421,纳入序列值计算表(表17.3)。
表17.3 玄始历闰周序列值计算表
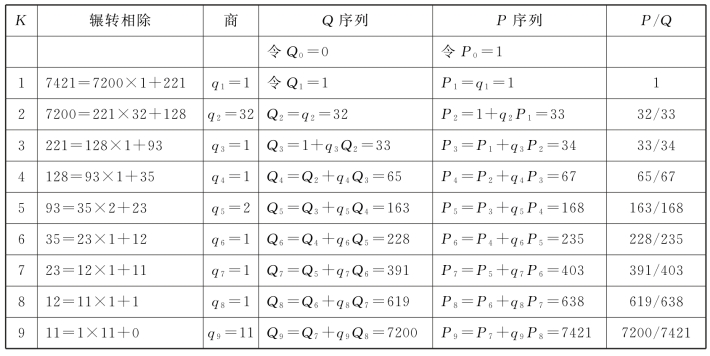
余数为0时,比值为7200/7421,与入算数组相同。如同本书11.3.5“入算数重现时的累积统计值”所说,我们增加此举是为保证序列值计算的成功。
但我们很难核查表中入算数据与导出数据,哪些经过了修改,出于什么考虑。
有趣的是东魏李兴业,同一组学者给出两组不同的闰周值:先是兴和历闰周562年207闰,每年为12.3683274月,替代北魏张龙祥等正光历的值。后来是九宫历的505年186闰,每年为12.36831683月,恢复到与北魏张龙祥等正光历的水平。
可见,没有更改的,只有李兴业手中的密近简化算法。
李兴业第一组的兴和历,即《甲子元历》(539年)。参与改历的人员规模之庞大,阵容之豪华,在中国历法史上非常罕见。计算如下(表17.4):
表17.4 兴和历序列值计算表
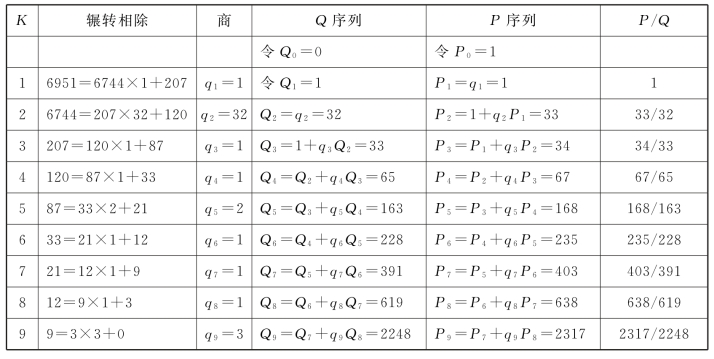
这里,6744/3=2248,6951/3=2317。最大公约数3,不影响序列值计算。除法余数为0时,比值为2248/2317。(https://www.daowen.com)
第二组九宫历的505年186闰,505×12=6060,6060+186=6246,每年为12.36831683月。计算如下(表17.5):
表17.5 九宫历、正光历序列值计算表
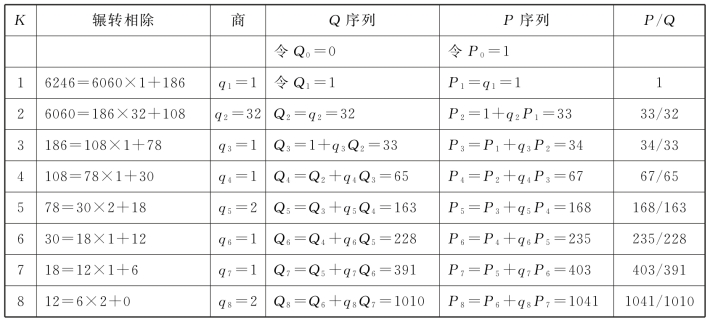
这里,6060/6=1010,6246/6=1041,最大公约数6不影响序列值计算。余数为0时,比值为1010/1041。
落下闳、刘歆的密近简化算法,适当选取原始数据,纳入密近简化算法,凭借某种信念在严谨的计算表中选取所需数据。在解决千年以来存在的闰周问题时,取决于测天的精度。
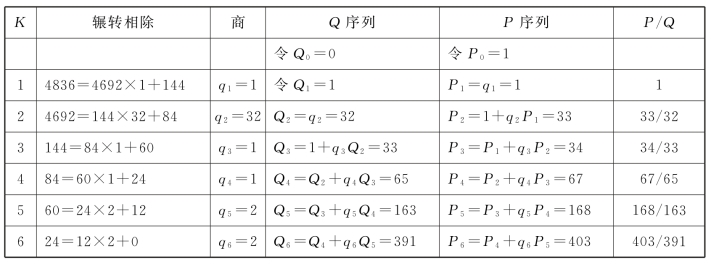
祖冲之大胆改革闰周,提出了391年144闰的新数据(表17.6)。
这里,391年×12=4692,4692+144=4836,4836/12=391,4692/12=403,最大公约数12,不影响序列值计算。余数为0时,比值为391/403。
表17.6 大明历闰周序列值计算表
公元前二世纪,人们就已习惯使用八尺(折合1.84 m)高表来测定冬至的日期。但是,靠八尺高表的读数并不理想。
祖冲之的贡献就是,不直接观测冬至那天日影的长度,而是观测冬至前后二十三四日的日影长度,再取它们的平均值,求出冬至发生的日期和时刻。由于离开冬至日远些日影的变化就快些,从而可以提高冬至时刻的测定精度。他的大明历岁实取365.2428日,在当时是很精密的。要到1064年明天历出现,采用更多的观测点,才能进一步提高精度。
在与权贵戴法兴的辩论中,祖冲之就是应用精密测定冬至点的方法,详细论证了19年7闰的闰周古法“其疏尤甚”[2]。他说:“古法虽疏,永当循用,谬论诚立……理容然乎?!”还说,日月五星的运行,“非出神怪,有形可检,有数可推”。只要精心观察并以历代记录来相互校验,“孟子以为千岁之日至可坐而知,斯言实矣”。从而对戴法兴的谬论“古人制章,立为中格,年积十九,常有七闰,晷或盈虚,此不可革”,指责的“削章坏闰”,污称的“恐非冲之浅虑,妄可穿凿”,进行了有力的驳斥。
古六历闰周19年7闰,岁有12.38642105月,玄始历600年221个闰月,岁有12.38633333月。大明历391年144闰,岁有12.368286445月,可见大明历闰法是胜过赵匪欠玄始历的。
所以,当今学者公认:“引进岁差和改革闰法为大明历的两大创法。”[3]支撑这一条的论据,一是改进测天精度,二是密近简化算法。
