10.2.1 剩余定理的背景
西方在16世纪以前采用的儒略历,由古罗马统治者儒略·西泽采纳天文学家索西琴尼的意见,制定于公元前46年。西泽的侄子奥古斯都,在公元前8年又做了调整。16世纪后期,罗马教皇格雷果里十三世加以修订,于1582年颁行,形成今天全世界通用的公历。
高斯文中提到的儒略年与儒略历不同,另指儒略日计日法,现代天文学用来计算年代相隔久远或不同历法的两事件之间所隔的日数。1583年,法国学者Scaliger,Joseph Justus(1540—1609)创立计日法,取名儒略,是为了纪念其父亲——意大利学者Scaliger,Julius Caesar(1484—1558)。
儒略日起点,规定在公元前4713年(天文学上记为-4712年)1月1日格林威治时间平午(世界时12:00)。每天一个唯一序数,顺数而下。例如:1996年1月1日12:00:00的儒略日是2450084。
高斯所提到的年序学观察示意图(图10.1),以小纪(A)、黄金数(B)和太阳循环周期(C)三个周期,分别度量起点到观察者测点的总时间段。三个周期的乘积15×19×28=7980年为儒略周期。
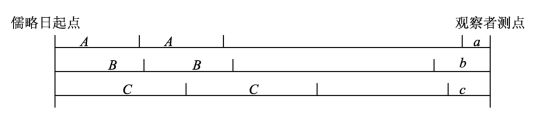
图10.1 高斯年序学观察示意图(https://www.daowen.com)
小纪(indiction cycle)15年(A):古罗马皇帝君士坦丁一世(Constantine,Ⅰ)颁布,每15年评定财产价值以供课税,成为古罗马用的一个纪元单位。
黄金数(golden number)19年(B),太阴周期,或称默冬章(Metonic cycle):经过一太阴周期19年,阴历月年的日序重复,就是235朔望月=19回归年。
太阳循环周期(solar cycle)28年(C):经过一太阳循环周期28年,星期的序与年的日序重复,就是365.25日×28=10227日=7×1461日,有1461个星期。
年序学观测中,保持小纪15(A)、黄金数19(B)和太阳循环周期28(C)三周期固定不变,对儒略日起点到观察者所测某点的时间段(z)进行不同次观测,得到的余数a,b,c值不同,有z≡a(mod A)≡b(mod B)≡c(mod C)。因模15,19和28固定,两两互素,直接相乘得固定总模7980。后续一系列α,β,γ值等,也都固定。如同高斯所说:“α就是6916。采用同样方法,我们求得β为4200,γ为4845,我们所求的数是6916a+4200b+4845c的最小余数。”这样,每次计算不必从头开始,只需把余数a,b,c填入6916a+4200b+4845c,再对总模7980取余数,就解出最小正整数解了。
这就极大地减轻了历法家的计算,高斯称之为“模板”。
一次同余式组问题中,非两两互素模的处理是个极大的难题。注意,模15,19和28只有两两互素,才能直接相乘得总模。
