8.7　欧拉定理

8.7　欧拉定理

欧拉函数φ（m） 设m是正整数，0，1，2，…，m中与m互素的数的个数，记作φ（m），称为欧拉函数。

当a本身是素数p时，φ（p）=p-1，例如，φ（13）=12。

如果a可分解成不同素因数的乘积

对一般的p，则须先分解成素因数再求出φ（p），例如，

p=225600=26×3×52×47,

故

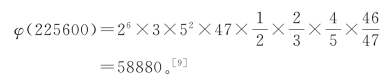
在古历会积题中，出现了

奇数=9253，定母=225600。

按大衍求一术计算，易从

k·9253≡1(mod 225600)

算得k=172717。

若依西法，则须计算N=9253φ（225600）=925358880，即使一台现代化的计算机，要完成这一计算任务也是不容易的。

欧拉函数解法

这里我们用欧拉函数解60x≡1（mod 13）这个数例。

解　m=13，素数，欧拉函数为φ（m）=12。

x=6012-1=6011=36279705600000000000。

可以核算：60×36279705600000000000≡1（mod 13）。

证明费马定理的方法也可用来证明以下费马定理的推广，这个推广叫作欧拉定理。

欧拉定理[10]设m为正整数，a为整数，当a与m互素时，则aφ（m）≡1（mod m）。

证明

作为欧拉定理的应用，有个系：设（a，m）=1，则同余方程ax≡b（mod m）的解为

x≡aφ(m)-1b(mod m)。

在系中，取a=Gi，m=ai，x=ki，并取b=1，这个系改写成：

设（Gi，ai）=1，则同余方程Giki≡1（mod ai）的解为