13.12.3 求元数筹算法
复原的依据 秦九韶摒弃开禧历家求元数算法，只简略描述为“闰赢，却与闰缩、朔率、元闰，列号甲乙丙丁四位，除乘消减，谓之方程，乃求得元数”。四个量的数理含义可以表示成3个并不互相独立的式子。令元数为x，朔数为y，有：
元闰×元数-朔率×朔数=闰缩， 377873x-499067y=188578，
元闰×元数-朔率×（朔数+1）=-闰赢，377873x-499067（y+1）=-310489，
闰缩+闰赢=朔率。 188578+310489=499067。
很有必要参照开禧历家、秦九韶所用数学工具，复原求元数402的可操作筹算法，以求窥见历家秘传的工具[27]。
筹算板布列的四数，与形式分数的三数相当（多出一个闰赢，下文讨论）；四数构成的整体与新引入变量相当；筹算板伴上相关商数，起着保留数据的直观作用。这三点是复原中最关键的考量。
对二元一次不定方程，不一定要用复杂的工具，用辗转相除法就可以解出[28]。下面第1除算图以元闰377873除闰赢、闰缩、朔率三项，相当于处理不定方程377873x-499067y=188578。用形式整数部分与形式分数部分之和表示x，即
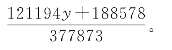
筹算板表示变量 形式分数部分恰巧反映在第2除算图中，相当于变量代换，令
。就是说，变量K1要用整幅筹算板表示成第2除算图。
变量的保留 形式整数部分y，连同四周所存商数，留待后续条件成熟之后，才能参与运算，于是保留在第1除算图左侧。就是说，第1归算图采用整幅筹算板，不但指变量y，也包括四周商数。
两列的形成 一次除算，必然布出左右两幅筹算板。朔率、元闰辗转相除，自然需要两列筹算板：一列除算图，另一列相同数量的归算图。
运算的转折点 第6图相当于求得158K4=559K5，158个K4与559个K5相等，齐同，于是设K4=K5=0，从除算转向归算。
全部运算见表13.5。为方便读者，附上字母变量解释、操作及去向。