13.5 近代数论核算
1966年,钱宝琮以近代数论核算开禧历。我们添加了一些注释,方便熟悉现代数论的读者,对照认识求入元岁术理。
证明中出现治历演纪题19个数据。这只能说明开禧历原题符合数论原理,却不能说钱宝琮的证明符合原意。特别是-24807这个负值,更说明了这一点。
这些证明中两次用到大衍求一术,这是直到1247年才由秦九韶创新出来的。1208年的开禧历只是用大衍术。
从上元甲子岁(A-)到嘉泰甲子岁(-I)的年数记为N。岁率6172608乘演纪积年N,满纪率1014000去之,不满,为气定骨193440,有
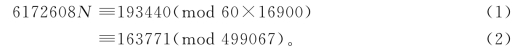
上元与嘉泰四年同是甲子岁,N能被60整除,设N=60n。又因6172608=365×16900+4108,故(1)式能写成
4108×60×n≡193440(mod 60×16900)。
“只以4108为斗定分,与日法,以大衍术入之,求得52为等数,144为因率,325为蔀率”(草),“以甲子60为纪法,乘等数,得3120,为约率”(草),
52×79×60×n≡60×52×62(mod 60×52×325)。
以60×52约,化简为
79×n≡62(mod 325)。
以79和325,用大衍求一术求得乘率144(79×144≡1(mod 325))。“以因率144乘之,得8928,满蔀率325去之,不满153”(草),
n≡62×144(mod 325)≡153(mod 325)。
“以纪法60乘之”(草),“得9180年,为入元岁”(草)。所以
N≡9180(mod 19500)(https://www.daowen.com)
或N=19500m+9180,m为正整数。
此时条件不成熟,没有使用合朔方面的数据,目标本是求出整体演纪积年,求出的只是其余数:入元岁,所以称“求入元岁之术”。
进一步,代入(2)式,6172608N≡163771(mod 499067),得
6172608(19500m+9180)≡163771(mod 499067),
因6172608=499067×12+183804,
183804×19500≡377873(mod 499067),
183804×9180≡-24807(mod 499067)。
(2)式化为
377873m-24807≡163771(mod 499067),
377873m≡188578(mod 499067)。
以377873与499067用大衍求一术,求得乘率457999,因得
m≡188578×457999(mod 499067),
m≡402(mod 499067),
N=19500m+9180。
上元到开禧三年丁卯岁,积年为N+3=7848183年。
