15.3.5 时曰醇求定数定理
时曰醇，字清甫，世为嘉定（今上海嘉定）人。其生平简述，见本书4.4“三色差分解法”。时曰醇的著作还有《今有术申》一卷及《求一术指》一卷，而《百鸡术衍》二卷为其代表作。
在《求一术指》（1861年）中，时曰醇的具体方法如下：
约分。任从问数中某位约起皆可。兹概从第一位起，约遍；又递用次位为主，与前后诸位遍约。……总之，两数相约不过一彼一此。初求得等，不妨任意约之。既约彼，仍有等，则反约此而乘彼，仍有等，再反约此而乘彼，必得之矣。
该方法中，实际上运行（1）子程序：以两个待约数求出约成数。（2）定向补偿：每步需要定向补偿素因数最高次幂。待约数如在三个以上，则运行（3）主程序：处理两两之间的子程序，使得两两互素。
今以数例演示子程序。
两个待约数，更相减损求出等数。以等数之值选择要约的数，定名为“彼”位。未约的另一个就叫“此”位。
例如，两个待约数A：54=2×33有最高次幂33=27，B：72=23×32有最高次幂23=8。更相减损求出最大公约数18=2×32。
用18化约，分成约B：72，约A：54两部分，比较各自的定向补偿素因数最高次幂。
先看18约B的部分，得到约成数“彼”a=54和“此”b=4。
乘积ab=54×4=216=23×33是A=54和B=72的最小公倍数。但a=54和b=4是相应待约数A=54和B=72的因数，54和4并不互素，只能称作准定数。
更有甚者，彼位B=72约去了18=32×2，成了b=4，破坏了素因数的最高次幂23=8。
两约成数a=54=2×33和b=4=22不一定互素。再次更相减损，彼位和此位之间有第二个最大公约数2，叫作续等。定向补偿素因数最高次幂。按法则，指定反约。“既约彼，仍有等，则反约此而乘彼”，此位上的54=2×33化约为27=33，而彼位上的4=22用续等2乘，得到8=23。
所丧失的待约数的素因数最高次幂23，就此凭借复乘而补回，得到8=23。
于是，约成数27和8，满足素因数最高次幂的要求，满足了定数三条件，成为定数。
现在再看18约A的部分，得到约成数“彼”a=3和“此”b=72。
乘积ab=3×72=216=23×33是A=54和B=72的最小公倍数。但a=3和b=72是相应待约数A=54和B=72的因数，3和72并不互素，只能称作准定数。
更有甚者，彼位a=3约去了18=32×2，破坏了素因数的最高次幂23=8。
两约成数a=3和b=72不一定互素。再次更相减损，彼位和此位之间有第二个最大公约数3，叫作续等。
按法则，指定反约。“既约彼，仍有等，则反定向补偿素因数最高次幂。约此而乘彼”，此位上的72=23×32化约为24，而彼位上的3用续等3乘，得到9=32。
所丧失的待约数的素因数最高次幂23，就此凭借复乘而补回，得到8=23。
两个待约数54和72，得到约成数27和8，满足素因数最高次幂的要求，从而满足了定数三条件。
处理所有问数间关系的主程序（3）。
上面两个待约数54和72，得到约成数27和8，满足素因数最高次幂的要求，从而满足了定数三条件。如果有三个待约数54，72，75，视作27与75第二组，8与75第三组，用子程序再算。最后，得到三个待约数的约成数，作为定数。
这些操作，用素因数概念来介绍似乎相当啰嗦，其实在筹算板上执行相当简单。下面的方括号仅仅表示处在筹算板上的同一组数据。
下面再举两例。
例如，对问数A：300和B：250，可演算如下。由于先约250，下边数位称为“彼”。
也可以先化约A，由于先约300，上边数位称为“彼”。于是
这里
表示用a和b的公因数（a，b）=d去化约a
现在我们以程行计地题为例，其中有三个问数A：300，B：240和C：180。采用素因数分解，A：300=22×3×52，B：240=24×3×5和C：180=22×32×5，可得定数A：25=52，B：16=24和C：9=32。
采用时曰醇的方法，有
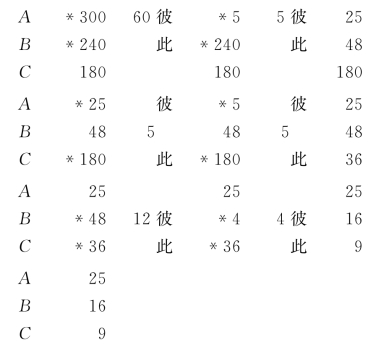
筹算板上留下A：25，B：16和C：9，就是求得的约成数。
1985年，在呼和浩特第二次全国数学史年会上，本人用近代数论概念表述和证明了时曰醇的这些话，并建议命名为时曰醇求定数定理[18]。
1995年，刘钝[19]指出，事实上，关于续等复乘的思想早已经出现在秦九韶的著作中，只不过时曰醇表达得更细致罢了。