18.4.3　奇序整数对数例

再举一个奇序整数对数例。借用婆什迦罗《莉拉沃蒂》第251诗节数据，求解附加数16的60x+16=13y。这里，60和13是奇序整数对。

我们先通过欧拉“x，y代入其他未知数”的变量分析法，得知附加数1的60x+1=13y的初解，x2=1时，有y3=1。再解出不定方程60x+16=13y。见表18.5。

表18.5　60x+16=13y的变量分析表

婆罗摩笈多没有变量代换，只能用辗转相除法的用语，刻画整除式。据术文2，“对余数单位1乘以一个所选择的数，使得乘积减去1（或者加上1，当商个数为奇数时），将可以由产生余数单位1的相应除数所整除”。自然余数1的除法是3=2×1+1，余数1乘以“所选择的数”x2，乘积1×x2“加上1”，除以除数2，取解式为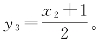

于是，取解式为，当x2=1时，有y3=1，这是初值。回代，x=8，y=37是不定方程60x+1=13y的一组特解。核算：60×8+1=480+1=481=13×37。

以x=8，y=37乘以16：x=8×16=128，y=37×16=592。除以对方系数后，得128=13×9+11，592=60×9+52。故不定方程60x+16=13y一组特解是x=11，y=52。核算：60×11+16=480+16=676=13×52。

可见，恒值粉碎机解法，能处理一切二元一次不定方程。