14.11　余米推数题

14.11　余米推数题

余米推数

问有米铺，诉被盗去米一般三箩，皆适满，不记细数。今左壁箩剩一合，中间箩剩一升四合，右壁箩剩一合。后获贼，系甲乙丙三名。甲称当夜摸得马杓，在左壁箩满舀入布袋；乙称踢着木履，在中箩舀入袋；丙称摸得漆椀，在右边箩舀入袋。将归食用，日久不知数。索到三器，马杓满容一升九合，木履容一升七合，漆椀容一升二合，欲知所失米数，计赃结断三盗各几何？

答曰：共失米九石五斗六升三合。

甲米三石一斗九升二合。

乙米三石一斗七升九合。

丙米三石一斗九升二合。

术曰：以大衍求之。列三器所容为元数，连环求等，约为定母。以相乘为衍母，以定各约衍母得衍数，各满定母去之，得奇。以奇定用大衍求得乘率，以乘衍数，得用数。次以各剩米乘用，并之为总。满衍母去之，不满为每箩米，各以剩米减之，余为甲乙丙盗米，并之为共失米。

本题关键是先求出每箩原有米数。以合为基本单位，涉及了下列一次同余式组：

N≡1(mod 19)≡14(mod 17)≡1(mod 12)。

三个模数两两互素，不必化约求定，也没有调用数的过程。

把余米推数题综合起来，为表14.21。

表14.21　余米推数题计算

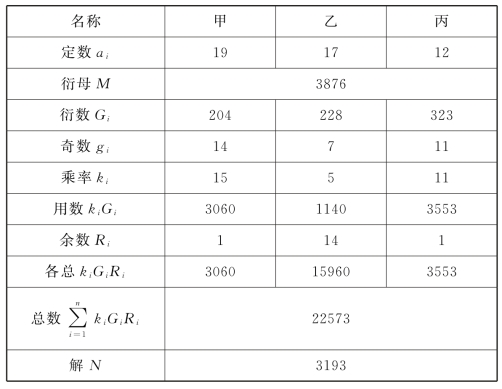
最小正整数解是N=3193合。

一只箩的容积3193合。扣除余下米数，三贼所盗米分别为3192合、3179合和3192合。

秦九韶采用最小单位“合”。按收数格，“命尾位分厘作单零，以进所问之数，定位讫”，最后，算得N=3193。再“展为”3石1斗9升3合，回复到原来的“收数”。