18.2.2　混淆取解式

18.2.2　混淆取解式

《库达卡与大衍求一术》[6]一文中，求解不定方程137x+10=60y，应用达生、辛格降系数不定方程的结论。文中所说“情况1.1.1”，就是达生、辛格的情况（ⅰ.1），设商个数为偶数，我们有r2n=1，r2n+1=0。

求解过程全录如下。

例1 137x+10=60y。

这里a=137，b=60，c=10，辗转相除得

q1=2,q2=3,q3=1,q4=1,q5=8,

r1=17,r2=9,r3=8,r4=1,r5=0。

从情况1.1.1，y2=q5t+10=8t+10，t可以随意选，如t=1=x2，得y2=18。

于是从下而上递推依次得回代过程是

y=q1x+y1=2×130+37=297,

x=q2y1+x1=3×37+19=130,

y1=q3x1+y2=1×19+18=37,

x1=q4y2+x2=1×18+1=19,

y2=18,

x2=1。

印度人氏习惯上把上面运算排成图式：

第一部分辗转相除和第三部分回代，不易犯错，关键在于取解式。

在本书18.3.3“用变量分析解137x+10=60y”中，我们分析了两种取解式。

自然余数取1，由新变量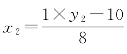，得整除式，有初解：取y2=18，则有x2=1。

余数为0，降系数不定方程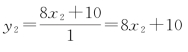中，有初解：取x2=1，则有y2=18。

库文中，用y2=q5t+10=8t+10，用到q5=8，余数r5=0，采用降系数不定方程取初解。我们看到，从“t可以随意选，如t=1=x2”，算得“y2=18”，明显不符合整除式取初解，即余数1初解的原术原意。见本书18.4“婆罗摩笈多的解法”。