14.3.2 原题原术
蓍卦发微
问:易曰,大衍之数五十,其用四十有九。又曰:分而为二以象两,挂一以象三,揲之以四,以象四时,三变而成爻,十有八变而成卦。欲知所衍之术及其数各几何?
答曰:衍母一十二,衍法三,一元衍数二十四,二元衍数一十二,三元衍数八,四元衍数六,已上四位衍数计五十。一揲用数一十二,二揲用数二十四,三揲用数四,四揲用数九,已上四位用数计四十九。
表14.1 阴阳象数示意图

大衍总数术,插入在题答和本题术曰之间。
本题术曰:置诸元数,两两连环求等,约奇弗约偶,徧约毕。乃变元数,皆曰定母,列右行,各立天元一为子,列左行。以诸定母互乘左行之子,各得名曰衍数。次以各定母满去衍数,各余名曰奇数。以奇数与定母,用大衍术求一[大衍求一术云,以奇于右上,定母于右下,立天元一于左上。先以右行上下两位,以少除多,所得商数,乃递互乘内左行,使右上得一而止,左上为乘率]。得乘率,以乘率乘衍数,各得用数。验次所揲余几何,以其余数,乘诸用数,并之,名曰总数。满衍母去之,不满为所求数,以为实。易以三才为衍法,以法除实,所得为象数,如实有余,或一或二,皆命作一,同为象数。其象数得一,为老阳;得二,为少阴;得三,为少阳;得四,为老阴。得老阳画重爻,得少阴画拆爻,得少阳画单爻,得老阴画交爻。凡六画,乃成卦。
算图1阴阳象数图,“始此四数以揲,终此四者为爻”。这是秦九韶的独创。
算图2中,天元1只是起乘法占位符的作用,以1,2,3,4四个数,构成互乘法,“互乘左行异子一,弗乘对位本子”。2×3×4=24,1×4×3=12,1×2×4=8,1×2×3=6,“各得衍数”24,12,8,6。算图3“以左行并之得五十”,达到“大衍之数五十”。
表14.2 算图1—算图3(https://www.daowen.com)
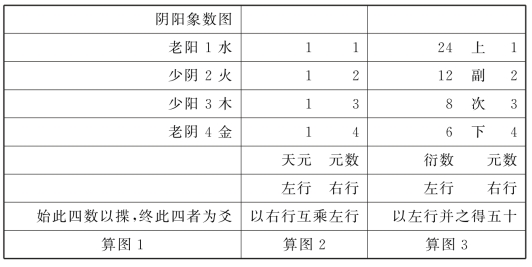
“故易曰大衍之数五十,算理不可以此五十为用。”扣去1,即成49。应阴阳伏数之说,能分得奇偶不同的两堆数的,只有奇数,这就“必须复求用数”49,“故先名此曰衍数,以为限率”。这是个限率,为51与49之间的选择,做个伏笔。
对1,2,3,4两两连环求等相约,得定母1,1,3,4,置算图4。再用互乘法,采用乘法占位符天元1,“互乘左行各子一,惟不对乘本子”,所得也“皆曰衍数”,置算图5。
表14.3 算图4—算图9
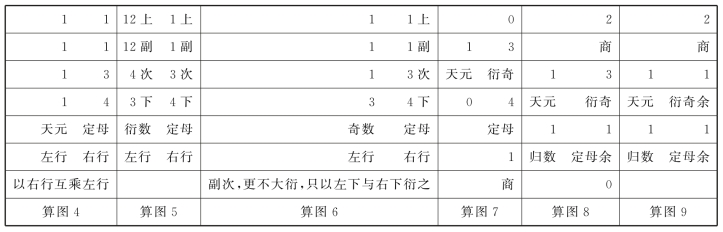
求定、求衍数(和为31,见算图11)、求衍母(12,见算图12)、求乘率,到求出四个泛用,按大衍总数术的一连串操作,最多只能求出四泛用之和:37(算图12)。为凑成49(算图13),需强添12,就回顾前面求等相约时,曾“推元用等数2,约副母2,为1”,“今乃复归之为2,遂用衍母12,益于左副12内,共为24”。大衍总数术中,这是常用的调用数过程。于是,“并之得49,名曰用数,用为蓍草数。故易曰其用四十有九是也。”
表14.4 算图10—算图15
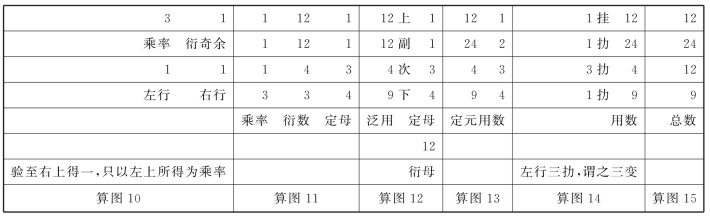
秦九韶极力推崇“必须复求用数”的49,理由是,只有奇数能分成奇偶不同的两堆数。这里,秦九韶重申这个理由,说能分得奇偶的数,只有49和51。如果默认51,会超出50,于是,只能“取七七之数”,非49不可。
接着,解释调用数。“始者左副二十四扐,益一十二,就其三十七泛为用数”,会产生两大缺陷:“三十七无意义,兼蓍少太露”,在周易上没有关于三十七的说法,且数量太少容易暴露意图。最后,调用数加以弥补。
