16.2.5 密近简化
西方数学发展史上大多数权威公认，连分数的近代理论开始于蓬贝利。
连分数尾部逐次删除，形成渐近分数系列。每个渐近分数的分子、分母是同一商qk相关的Pk，Qk序列值。
现代数论教科书[9]上有这样的渐近分数定理：
定理 若连分数[q1，q2，…，qk]的渐近分数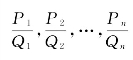
，则在这些渐近分数之间，下列关系成立[注：这里我们已经假定各渐近分数是存在的。事实上，当q2=0（或q2q3+1=0）时
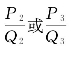即不存在]：
P1=q1,Pk=qkPk-1+Pk-2,k=3,…,n,
Q1=1,Qk=qkQk-1+Qk-2,k=3,…,n。
可见，渐近分数并非只有一种求法。随着辗转相除的展开，各商所对应的两个P，Q序列之比也会形成渐近分数。
1208年的求乘率筹算原图深深地刻着发展进程的烙印，它涉及三阶段的整数对现象：两整数辗转相除得一系列商，为第一阶段；第二阶段计算的只是单组Q序列值；第三阶段依据某条件，关联某序列值为所需的乘率。此时的入算两整数，或为线性不定方程两系数，或为线性同余式系数与模，或来自传统数学满去式。
为适应古代历法编排，古人需要简化渐近分数的分母，简化渐近分数的分子，而使得渐近分数维持尽可能精确的值，不妨称为密近简化算法。密近指与原比值之差的微小程度，简化特指分子、分母位数的减少。
现在我们理解了1208年的开禧历，掌握了大衍术背后的整数对现象。
通过剖析公元前7年三统历的大周概念，确认公元之前的落下闳、刘歆已经掌握了密近简化算法。在史实上，密近简化算法的出现先于求乘率术。但在数理上，密近简化算法内含于上元积年求乘率术。
正是整数对现象发展的内在逻辑，支撑我们跨越上下4000年，探索上元积年的本原。
然而，这只是说到数理上的存在性，我们还要考虑传统数学筹算方面的构造性。因为根据1208年的开禧历分析此前1215年的三统历只是臆想。
如果没有发现以岁星岁数为代表的大周概念，我们真不知道怎样跨越开禧历之前1200多年的漫长时光，去证明公元之初历法家已经知晓密近简化算法。
天象观测呼唤数学，推动数学，反过来，数学进步又会深化人们对天象的认识。
我们相信，以开禧历、三统历相关史料为基础，依据整数对现象的内在逻辑一步步向远古探索，有可能追溯上元积年的本原，有希望窥见中华文明的曙光。