15.4.2 张敦仁大衍求一
2026年01月14日
15.4.2 张敦仁大衍求一
张敦仁(1754—1834),字古余,山西阳城人,其《求一算术》三卷(1803年)中的求乘率方法,原文如下:
大衍求一(以乘率乘少数,满多数去之,必余一,犹大衍之奇一,故曰大衍求一)
术曰:列少数于上,多数于下,所得为第一数。有余,复以下除上,所得为第二数。如是上下相除,所得以次命之(如第三数、第四数之类)。上位余一(如上位除尽,即减得数一为余一;如上位五,下位一,常法以一除五,得五,除尽。此术以一除五,则为四,余一,与常法不同)即止不除。乃列各得数于左行,立天元一为右行第一数,以左行第一数乘之,得右行第二数(此无上位可加,故即为第二数)。复置右行第二数,以左行第二数乘之,加入右行第一数,得右行第三数。每置右行数,以左行相当之数乘之(谓第一第二位数相当),以右行上位加之,得右行次位(右行位数恒多于左行一位。如左行有四数,右行即有五数,此第五数即乘率也)。
今按照张敦仁的大衍求一法演算(图15.2)。
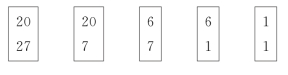 (https://www.daowen.com)
(https://www.daowen.com)
图15.2 张敦仁大衍求一术的演算
辗转相除后,左右行记下商数、天元一,称作第一数、第二数……(表15.1)
表15.1 张敦仁大衍求一术的分析

