11.6.2　奇偶配置

11.6.2　奇偶配置

余数为1的商个数的奇、偶和不定方程ax=by±1中常数1的正、负，会出现四种并列的情况，标识成[奇正]、[偶负]、[奇负]和[偶正]。参见表11.6。

表11.6　奇、偶序整数对与四种不定方程的可能解配置

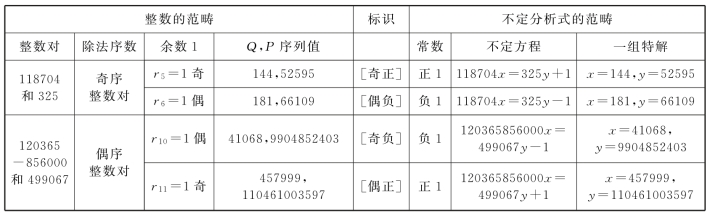
传统历法只关心常数正值的满去式，相当于[奇正][偶正]的两组关联。

不定方程与一次同余式等价，还可进一步推衍到传统数学的满去式。

辗转相除过程的一般项以字母k标记，形成自然数数列。由k奇偶交替，（-1）k值正负交替，奇偶分析法能够分析交替出现的性质。

鉴于除法次数（商个数）的非奇即偶，自然余数除数序数的非奇即偶，常数1的非正即负，筹算位的非上即下、非左即右，我们可以依据一方的研究，推测到另一方的结论。

高斯抓住余数为0时的商总个数n，称为项的个数，建立配置法则：

当[α，β，γ，…，μ，n]项的个数是偶数时，我们有ax=by+1；当[α，β，γ，…，μ，n]项的个数是奇数时，我们有ax=by-1。

我们则抓住自然余数的商个数，比余数0的商总个数n少1。

于是，高斯配置法则可修改成：自然余数的商个数n-1是奇数时，即商总个数“是偶数时，我们有ax=by+1”。自然余数的商个数n-1是偶数时，即商总个数“是奇数时，我们有ax=by-1”。