8.4.2　常数永远不变

8.4.2　常数永远不变

解二元一次不定方程，两个互素的系数辗转相除，到自然余数1为止。所涉及的常数如何处理会构成各色各样的解法方案。

罗尔的指导思想是，坚守作为整数的常数，数值及符号保持永远不变。

本例中，两系数辗转相除应该有三步得到自然余数1。

首先，不定方程12z=221h+512的大系数221，除以较小系数12，商是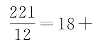。利用整数18，引入新变量h：“设z=18h+p”，代入12z=12（18h+p）=216h+12p=221h+512。我们得到新不定方程12p=5h+512。常数512连加号都不变。

第二步，两个系数中，12除以较小的5，商中整数是2，引入新变量h=2p+s，得到新不定方程2p=5s+512。同样，常数512前保持加号的特点。

第三步，引入新变量p=2s+m，有2m=s+512。

“得到一个系数为1的变量s”，实质是，辗转相除出现了自然余数1。

逐步回代：s=2m-512，p=2s+m，h=2p+s，z=18h+p。

于是，得到原不定方程的全部解：

z=221m-47104,h=12m-2560。

里面含有的m是整数。