11.2.3　降系数不定方程分析

11.2.3　降系数不定方程分析

我们在本书9.3节“形式分数的分母值取1”中，已经初步分析欧拉整数解思想。现在进一步列出降系数不定方程分析表，为研究印度数学史打下基础。

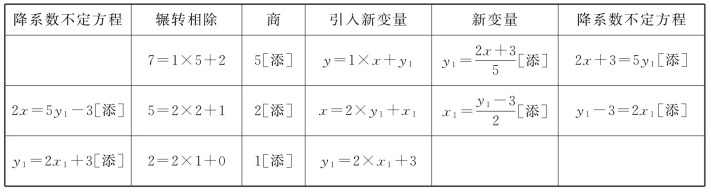
在表11.1降系数不定方程中，用“添”字标记新增添的各项。

先看列。第三列为商5，2，1。第五列引入的新变量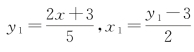，都是形式上的分数、实质上的整数。整理新变量得第六列，为降系数不定方程2x+3=5y1，y1-3=2x1。第六列的降系数不定方程2x=5y1-3，y1=2x1+3，演变成第一列。

再看行。第一行出现新变量y1，第二行出现x1。第三行y1=2×x1+3是降系数不定方程，3不再是变量，此处与余数0相关联。

表11.1　降系数不定方程

欧拉求的是通解，带有一个参数x1，表示了不定方程的全部解。

余数为0，有降系数不定方程y1=2x1+3。取x1作任意整数，转入回代，得通解：x=5x1+6，y=7x1+9。

通解求出来，给出参数，就是特解。

我们取x1=1，有y1=5。逐步回代，x=11和y=16是不定方程5y=7x+3的一组特解。

降系数不定方程的背景是余数为0的现代辗转相除法。