14.10.1 原题原术
积尺寻源
问欲砌基一段，见管大小方甎、六门、城甎四色。令匠取便，或平或侧，只用一色甎砌，须要适足。匠以甎量地计料，称用大方料，广多六寸，深少六寸。用小方：广多二寸，深少三寸。用城甎，长：广多三寸，深少一寸；以阔：深少一寸，广多三寸；以厚：广多五分，深多一寸。用六门甎，长：广多三寸，深多一寸；以阔：广多三寸，深多一寸；以厚：广多一寸，深多一寸。皆不合匝，未免修破甎料裨补。其四色甎，大方，方一尺三寸；小方，方一尺一寸；城甎，长一尺二寸，阔六寸，厚二寸五分；六门，长一尺，阔五寸，厚二寸。欲知基深广几何？
答曰：深三丈七尺一寸，广一丈二尺三寸。
术曰：以大衍求之。置甎方长阔厚为元数，以小者为单，起一。先求总等，存一位，约众位[列位多者，随意立号]，乃为元数。连环求等，约为定母。以定相乘为衍母。各定约衍母得衍数。满定去之，得奇。奇定大衍，得乘率。以乘衍数得用数。次置广深多少，数多者乘用，少者减元数。余以乘用，并为总。满衍母去之，不满，得广深。
今需砌一处长方形房基（一边称作广，另一侧边称作深），现有四种砖料：大方料，各边皆为11尺3寸；小方料，各边长1尺1寸；城砖，长、宽、厚各为1尺2寸、6寸和2寸5分；六门砖，长、宽、厚各为1尺、5寸和2寸。请匠人任取一种砖料，使砌基时都用整砖，砖可正置，也可侧置。匠人测量知，无论用何种料，都不能恰好全用整料，需用破砖裨补。根据所列出的数据，求该房基的广、深各是多少。
这个问题可由一次同余式组表示：
N≡60(mod 130)≡20(mod 110)≡30(mod 120)≡30(mod 60)
≡5(mod 25)≡30(mod 100)≡30(mod 50)≡10(mod 20),
此式满足可解条件。
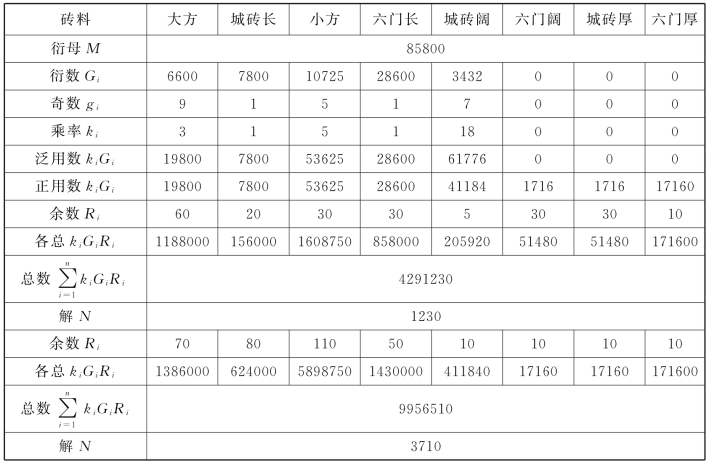
把8个数据从小到大排列，以砖色为序列出数据来命名，如下表（表14.16）：
表14.16 砖色为序命名表
把全题综合起来，见表14.17。
表14.17 积尺寻源题计算综合
续表
