10.4.1 用数计算
沿着1881年马蒂生走过的路，我们分别用1801年高斯和1247年秦九韶的方法，试算公元4世纪的物不知数题，观察所出现的伴随数与用数，加深理解。用高斯剩余定理，写成一次同余式组：
z≡2(mod 3)≡3(mod 5)≡2(mod 7)。
关键一步，就是轮流以A=3，B=5，C=7为模，构造常数1同余式，以“（BCD等）x≡1（mod A）的一个解（最好是最小值）”，再用BCD等其他模所乘，求出相应伴随数：
构造5×7x1≡1（mod 3），解出x1=2。再乘以5×7，α就是70。
构造3×7x2≡1（mod 5），解出x2=1。再乘以3×7，β就是21。
构造3×5x3≡1（mod 7），解出x3=1。再乘以3×5，γ就是15。
求总模3×5×7=105后，才用余数a=2，b=3，c=2代入z≡αa+βb+γc+δd等（mod ABCD等），有
z=70（α）×2（余数）+21（β）×3（余数）+15（γ）×2（余数）=233，
z=233-2×105=23。
于是，物不知数题可表示成表10.4。
大衍总数术一般处理非两两互素模题。解物不知数题，相当于解两两互素模的余米推数题。以表格形式表达，三项称为甲、乙、丙。所附数学史界通用字母符号，仅供检索。其中，衍数记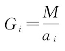
，以p记任意整数，最小正整数解为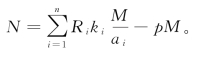
表10.4 大衍总数术解物不知数题
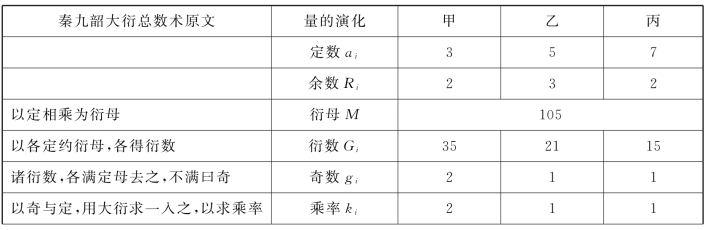
续表
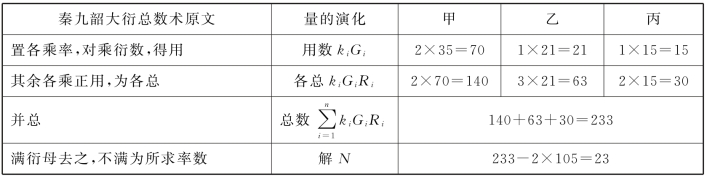
乙、丙项奇数为1，乘率径自为1。甲乘率的计算，以衍数5×7=35和定数3先求出奇数2，再与定数3入大衍求一术。下面算图（图10.2）右上得1时，检视左上2，就是乘率。
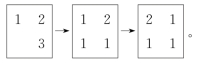
图10.2 大衍求一术算乘率示意图
同样的数值70，21，15，到高斯解法中体现α，β和γ伴随数概念，到秦九韶大衍总数术导致“用数”概念，到明代孙子歌中成了口诀：“三人同行七十稀，五树梅花廿一枝，七子团圆正月半，除百令五便得知。”