5.7 同余的性质
定义 令m为非零整数，a和b是整数，如果a-b是m的倍数，我们说a，b关于模m同余，表示为a≡b（mod m），也就是说，当a和b都用m除时，余数相同。
不难看出，a≡b（mod m）⇔a≡b（mod（-m）），从而今后只讨论m为正整数的情况。
例如，5≡2（mod 3），-1≢6（mod 8）。
显然，a≡0（mod m）⇔m|a。
同余式有以下的性质：
引理1 同余关系是等价关系，也就是说：
（ⅰ）（反身性）a≡a（mod m）。
（ⅱ）（对称性）如果a≡b（mod m），那么b≡a（mod m）。
（ⅲ）（传递性）如果a≡b（mod m），b≡c（mod m），那么a≡c（mod m）。
例如，25≡19（mod 6），19≡13（mod 6），那么25≡13（mod 6）。
证明 （ⅰ）和（ⅱ）是显然的。对于（ⅲ）：由于a≡b（mod m）和b≡c（mod m），可知m|a-b，m|b-c，从而m|[（a-b）+（b-c）]即m|a-c。因此a≡c（mod m）。
引理2 如果a≡b（mod m），x≡y（mod m），那么
（ⅰ）（等式求和差性）a+x≡b+y（mod m）和a-x≡b-y（mod m）。
例如，25≡19（mod 6），13≡7（mod 6），那么25±13≡19±7（mod 6）。
（ⅱ）（等式相乘）ax≡by（mod m）。
例如，25≡19（mod 6），13≡7（mod 6），那么25×13≡19×7（mod 6）。
证明 由a≡b（mod m），x≡y（mod m），可知m|a-b，m|x-y，于是m|a（x-y）+y（a-b）=ax-by。因此ax≡by（mod m）。
必须指出，一般而言，等式的两边除以同一个数，等式不成立。
例如，6≡8（mod 2），但3≢4（mod 2）。
（ⅲ）对于每个整数k，ka≡kb（mod m）。
引理3 设ac≡bc（mod m），则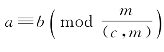
。特别地，若（c，m）=1，则由ac≡bc（mod m）得到a≡b（mod m）。
证明 由引理的条件可知m|ac-bc=（a-b）c，于是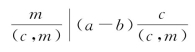
。由于
这是等式的除法。这个引理的另一个表示法是：如果ac≡bc（mod mc），c≥1，那么a≡b（mod m）。
例如，21≡15（mod 6），3×7≡3×5（mod 3×2），那么7≡5（mod 2）。
引理4
（ⅰ）（关于模的因数）如果a≡b（mod m），m被d整除，d≥1，那么a≡b（mod d）。
例如，25≡19（mod 6），6被2整除，那么25≡19（mod 3）。
（ⅱ）如果a≡b（mod m），那么（a，m）=（b，m）。
证明 由条件知存在整数x使得a=b+mx，于是（a，m）=（b+mx，m）=（b，m）。
(ⅲ)a≡b(mod mi)(1≤i≤r)⇔a≡b(mod[m1,m2,…,mr])。
证明 由（ⅰ）知“⇐”是成立的。
另一方面，如果a≡b（mod mi）（1≤i≤r），则mi|a-b（1≤i≤r），即a-b是m1，m2，…，mr的公倍数，从而a-b是[m1，m2，…，mr]的倍数，即a≡b（mod[m1，m2，…，mr]）。