14.4.2 开禧历会积题
术文尾部说:“今设问以明大衍之理,初不计其前多后少之历过。”多,指历过年数9163多。少,指未至年数9077年少。只指两数比较,与“大衍之理”有什么关系?正是这一句含有的奥妙,促使我们编出开禧历会积题,揭开古历会积之谜。
现在用开禧历数据列出题问,再以古历会积的解法解答,自编一个开禧历会积题:
今有日法:“一万六千九百为日法。”岁率:“六百一十七二千六百八为岁率。”朔率:“四十九万九千六十七为朔率。”纪率:“纪率一百一万四千。”气定骨:“以一十九万三千四百四十为气定骨。”朔定骨:“二万九千六百六十九,为朔定骨数。”
欲求开禧历气朔甲子一会,积年积月积日,及历过未至年数各几何?
从遥远的上元到近期编历岁,满去岁率,气余数为0,这是求岁周法。相应地,时间总量满去朔望月,月余数为0,可称求月周法。时间总量满去日名干支周期纪法,纪余数为0,求日名干支周期个数,那就只能称求纪周法了。
开禧历求的是岁周,气余数为0。
开禧历整数论的基础:日法16900,其取值,保证大衍术各数据,以整数的形式运算。
这里求定数,只需要用最方便的素因数分解法。6172608=26×13×7419,499067=499067,1014000=24×3×53×132,化得474816为气定,499067为朔定,21125为纪定。
现以表格形式计算如下(表14.6):
表14.6 开禧历会积题的演算
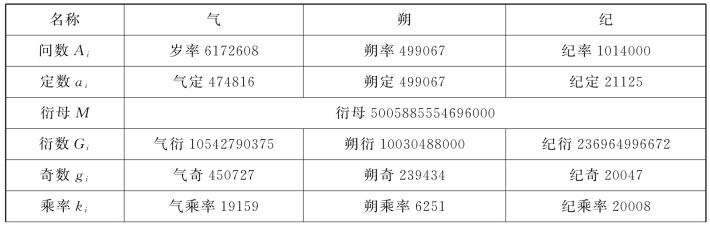
续表
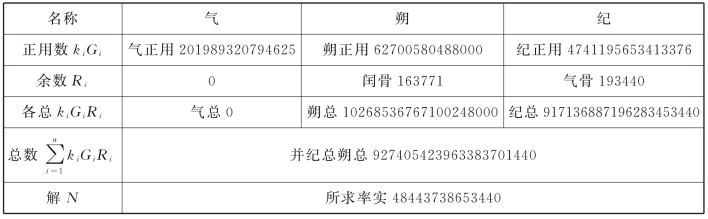
这就呈现一个三段演算过程,分别以衍母、正用和历过年数为标志。
1 以衍母为标志的求会积
由岁率6172608、朔率499067和纪率1014000,求得气定474816,纪定21125,朔定499067。三定相乘,得衍母5005885554696000。(https://www.daowen.com)
衍母除以气分,即岁率6172608,得一会积年810983875岁。除以朔分499067,得一会积月10030488000月。除以纪分1014000,得一会积纪4936770764个纪周。除以日法16900,得总积日296206245840日。
只要气朔纪长度确定,衍母就确定,积岁积月积日就确定。
2 以正用为标志的求用数
各定数约衍母,得衍数。各衍数满定数去之,得奇数。气奇、朔奇和纪奇各与相应定数,用大衍求一术,各得气乘率19159、朔乘率6251和纪乘率20008。分别对乘相应的气衍、朔衍、纪衍:气正用201989320794625,朔正用62700580488000,纪正用4741195653413376。
只要气朔纪长度确定,三个正用数就确定。
3 以历过未至年数为标志的余数处理
气骨193440×纪正用4741195653413376=917136887196283453440纪总。
闰骨163771×朔正用62700580488000=10268536767100248000朔总。
气余数0×气正用201989320794625=气总0。
纪总+朔总+气总0=927405423963383701440,满衍母5005885554696000,所求率实为不满48443738653440。所求率实48443738653440÷气分6172608=7848180岁,为历过年数。
一会积年810983875岁-历过年数7848180岁=未至年数803135695岁。
历过年数7848180(少)处于一会积年810983875岁的前部,未至年数803135695(多)处于后部。相比于古历会积的“前多后少”,这可说成“前少后多”。
4 我们的认识
阅读上面的数据演算时,不免有一种腾云驾雾之感。见到熟悉的数字“7848180”时,我们才会恍然大悟,演纪积年就是相对于气朔甲子一会之数的历过年数。
“气朔甲子一会,积年积月积日”,衍母是气朔甲子的最小公倍数。从周期度端讲,衍母体现一个会字。从周期长度讲,根据所有涉及气朔甲子周期,齐同而得的总周期,衍母体现一个积字。而用求岁周法算历过年数,一下子就得到了演纪积年。
开禧历中,上元只是作为基本周期回归年、朔望月、干支纪日、干支纪岁与所齐同大周期的总起始端。
