14.12.6 复数格的原型
从原文、原术、原意的角度说来,我们可以看到,复数格前五句的原型就是程行两题[19]。
下表(表14.23、表14.24)中,标有星号的数指含有等数的待约数。待约数右边圆括号标的数指等数。圆括号中带乘号的数指续等,用来复乘。
例如,程行计地题草术分析表(表14.23)第二行左起第四格为例,圆括号标的数3是300和3的等数,这个续等3,约300为100,复乘其所对应左边的3。
表14.23 程行计地题草术分析表
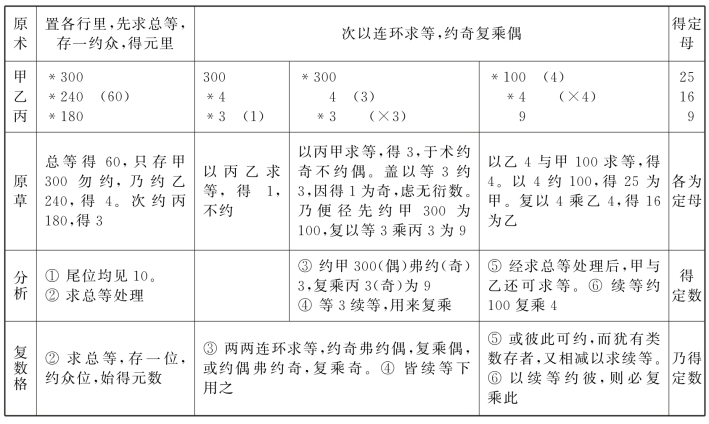
表14.24 程行相及题草术分析表
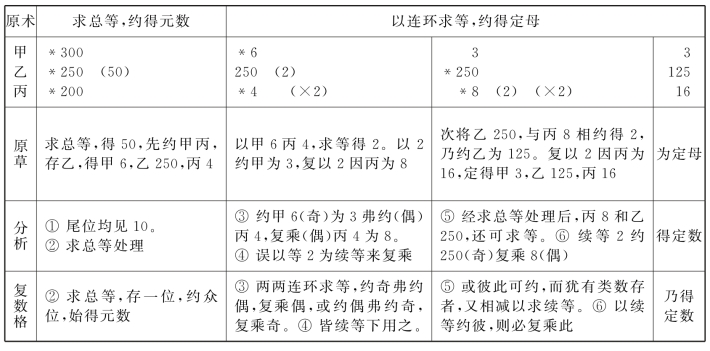
两张分析表中,依次标上序号。现按序号分析如下;
①复数分类中,特地指明“急足之类”,即程行两题。复数格第一句“复数者,问数尾位见十以上者”,只有程行两题。
②秦九韶在问数分类时说过元数、复数的区别:元数,谓尾位见单零者。复数,谓尾位见十或百及千以上者。“复数者”300,240,180和300,250,200,求总等处理后,得300,4,3和6,250,4,“始得元数”。(https://www.daowen.com)
③两两连环求等过程中,程行计地题,“于术约奇不约偶”改为“约甲300为100”,即约偶不约奇。而程行相及题,“以2约甲为3”,因甲6(奇)丙4(偶),为约奇不约偶。
显然,复数格“约奇弗约偶”“或约偶弗约奇”直接取决于两题,并非特意对仗。
④“皆续等下用之”的“皆”字,指两题。对照第③条,意味深长。
⑤第一次复乘之后,程行计地题250与8,程行相及题100与4,都还有等数。秦九韶笔下的“或彼此可约,而犹有类数存者”,相当于我们今天说,如果还有进一步的等数。“彼此可约”是现象,“犹有类数存者”是本质。
⑥“以续等约彼,则必复乘此”,普遍适用。
再对照复数格的原文:
复数者,问数尾位见十以上者。以诸数求总等,存一位,约众位,始得元数。两两连环求等,约奇弗约偶,复乘偶,或约偶弗约奇,复乘奇,皆续等下用之。或彼此可约,而犹有类数存者,又相减以求续等。以续等约彼,则必复乘此,乃得定数。所有元数、收数、通数三格,皆有复乘求定之理,悉可入之。
秦九韶对从“程行”两题归纳出的复数格,有个总体认识:求总等,“始得元数”之后,必然是紧连着“两两连环求等,约奇弗约偶,复乘偶……”的。基于这样的认识,在14.4.3“古历会积原题”中,秦九韶特意交代:本题求总等后,本当“复乘偶”,仅因“本题欲求一会”,故“不复乘偶”了。
反过来,程行相及题问数是300,250和200,正确的定数应该为3,125和8。
秦九韶处理成:因三数有总等50,下一步求出6和4的最大公约数2,就误认作续等。于是续等复乘,产生了4×2=8。最终成了3,125和16。这是太迷信复数格了。
