17.4.3 祖冲之不等式推算
许多数学家和数学史家往往用一种方法解释约率
、密
，再用另一种方法解释胬数3.1415926、盈数3.1415927，两法彼此割裂。
查有梁[15]先生解释祖冲之缀术，乃补缀之术、逼近之术，逼近正圆。提出的缀术求π新解，令人耳目一新。我们赞成查有梁的连分数渐近分数说，只是换成落下闳、刘歆的密近简化法，展示的是序列值计算表。
我们以为，祖冲之可能利用刘徽割圆术的“差幂”，实行补缀衔接，应用密近简化法，简捷明快求出胬数、盈数。再用密近简化法求出约率、密率。
现在观察圆面积算式
中，处于差幂（S192-S96）之前的系数。设
，圆面积算式成了S≈S192+β（S192-S96）。
人们常说的刘徽不等式为
右边过剩值是S2n+β（S2n-Sn）。左边不足值补缀上α倍差幂，规定α小于β，成为S2n+α（S2n-Sn），就得到祖冲之不等式：
其中，α＜β为待定系数。
从圆内接正多边形S192入手，算出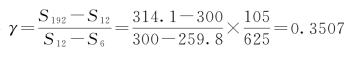
。有序列值计算表（表17.9）。
表17.9 3507和10000序列值计算表
续表
以3522和10000纳入序列值计算，得到表17.10。
表17.10 3522和10000序列值计算表
因S3072=3.14159046，S1536=3.14158389，计算的中间数值，我们精确到小数点后八位，有
只要到圆内接正3072边形，这样一组3.14159265和3.14159278，在舍去0.00000005和0.00000008之后，恰巧与《隋书·律历志》中记载七位的（胬数）3.1415926和（盈数）3.1415927相吻合。但这肯定不是四舍五入，出于什么考虑，我们无法想象。
祖冲之不等式（2）、（3）实质上是一种逼近法、外推法，α，β为待定的外推系数。外插法与内插法实质是一样的。内插法是从某函数的一组已知值去求出另一中间值的方法。如果所求函数值是位于已知的一组值的区域之外，则应用外推法求之。
祖冲之不等式表明，祖冲之的缀术是补缀之术、逼近之术。包括分数逼近（连分数渐近分数）、代数-几何逼近（割圆术）、函数逼近（外挂法）。这就是祖冲之缀术求π的贡献所在。