16.6.3　终而率之算法

16.6.3　终而率之算法

岁星与太阳每经6136091496岁重合5621200000次。这个大周分子分母数值太大，不适合编制历法，需要简化。这种需求催生了密近简化算法。

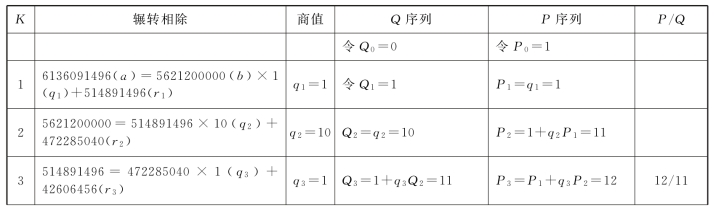
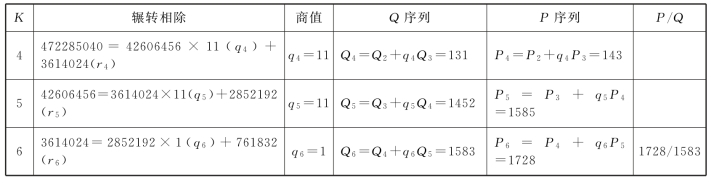
我们采用序列值计算表，计算6136091496和5621200000如下（表16.4）：

表16.4　6136091496与5621200000序列值计算表

续表

刘歆发现，1728是12的144倍，与《周易·系辞》的“坤之策百四十有四”相符。在纪母中，明确坤（巛，坤字古体）策144：“木金相乘为十二，是为岁星小周。小周乘巛策，为千七百二十八，是为岁星岁数。”

1728岁1583见，密近于6136091496岁5621200000见，数值相差0.00000007。分子、分母简化成四位，有利于历法编排。我们称之为密近简化算法。

从古代相传的岁星12年11见，通过相约算法得到6136091496岁5621200000见，最后用密近简化算法调出1728年1583见，都是岁星大周，都由三交点所界定，都是日出时岁星现于东方地平线上某背景点此天象的再次出现。

尽管从现代数学的严格观点看，密近简化算法前后的两个三交点，还是有所偏移的。

三统历假托黄钟，附会易著，玄妙其词，宗旨是宣扬皇权神授，巩固政权，稳定社会。刘歆刻意凑合岁星岁数，挂靠周易“乾坤之策”。这个荒诞之举，竟成了现今人们不可或缺的史料，证明公元交替时期历法家流行着一种密近简化算法。

一般地说，同一序列中较大的值，除非刻意凑合，不可能是较小值的倍数。刘歆要找出“木金相乘为十二，是为岁星小周。小周乘巛（坤字古体）策，为千七百二十八，是为岁星岁数”。只有刻意放弃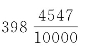，改成