18.4.1 原术原意
婆罗摩笈多（Brahmegupta，梵藏，约598—约665），早期乌贾因（Ujain）学派代表，628年著有《婆罗摩修正体系》。655年完成另一本天文著作。
狄克逊英文版《数论史》所列史料，夹叙夹议，介绍婆罗摩笈多术文和数例二，讨论恒值粉碎机。所列文献原始信息抄录如下：Brahme-sphut'hánta，Ch.18（Cuttaca=algebra），Colebrooke，pp.330-331。
我们先录《数论史》英文，再全译如下：
Brahmegupta(born 598 A.D.)gave the following rule to find a constant“pulverizer”.From the given multiplier and divisor,remove their greatest common divisor(found by mutual division).The thus reduced multiplier and divisor are mutually divided until the residue unity is obtained,and the quotients are written in order.Multiply the residue unity by a number chosen so that the product less one(or plus one,if there be an odd number of quotients)shall be exactly divisible by the divisor which produced the residue unity.After the above listed quotients place this chosen number and after it the quotientjust obtained.To the ultimate add the product of the penultimate by the next preceding term[etc.].The number found,or its residue after division by the reduced divisor,is the constant pulverizer.
术文分成三段，我们依次编号。
婆罗摩笈多（梵藏）（生于公元598年）叙述了寻找恒值“粉碎机”的法则。（术文1）根据已知的乘数和除数，用（辗转相除法找到的）最大公约数，加以约简。如此约简后的乘数和除数辗转相除，直到余数单位1而止，并依次记下商值。（术文2）对余数单位1乘以一个所选择的数，使得乘积减去1（或者加上1，当商个数为奇数时），将可以由产生余数单位1的相应除数所整除。（术文3）在上列商值之下，放置这个所选定的数，此后再放置刚求得的商值。对于最后数，加上中间数与下一个前置项的乘积（等等）。所找到数，或其经约简除数的除法之后的余数，就是恒值粉碎机。
数例二讲述阿耶波多不定方程137x+10=60y。同样分成三段，依次标明。
Again(§27,p.336),let the reduced dividend[multiplier]and divisor be 137 and 60,while the augment or additive quantity is 10.By reciprocal division of 137 and 60,we get the quotients 0,2,3,1,1 and last two remainder 8 and 1.Since the augment is now positive and the number of quotients is odd and since 1·9-1 is divisible by 8,we select 9 as the chosen number.The constant pulverizer is said to be found as before.Its product by 10 is divided by 60 to give the desired multiplier 10;10·137+10=60·23.
又（§27，p.336），（数例二1）设约简的被除数[乘数]和除数为137和60，而增加或附加数为10。通过137和60辗转相除，我们得到商值0，2，3，1，1，最后两个余数是8和1。（数例二2）因为附加数现在为正，商个数为奇数[见下面的译者注]，又因为1×9-1可被8整除，我们选9作为选定数。（数例二3）据说可如前一样找到恒值粉碎机。它与10的乘积可被60除，以得到所需的乘数10；10×137+10=60×23。
我们知道137x+10=60y。两系数137和60辗转相除到余数1时的商个数4是偶数。增加了商为0的除法60=137×0+60，余数1的商个数从4增加到5，成了奇数。
这里要讨论一下术文“已知的乘数”、“如此约简后的乘数”、数例二题首“被除数[乘数]137”，都是指所求未知数x。题尾计算所得的“所需的乘数10”，即x=10，则是阿耶波多不定方程的解。印度数学史的注释中，公认库达卡解释为“乘数”[7]，记为x。可见，库达卡所指，似乎过于广泛。
1 单位1的关联
术文第一段，利用1构作整除式，需要两系数重复两次辗转相除，保证得到余数1。当然，还需要利用附加数非常数1的原不定方程，构作附加数1的不定方程。
单位1的作用、余数1与附加数1的关联早在6世纪时的婆罗摩笈多的恒值粉碎机解法中就体现出来了。
我们在18.3.1“序列值解法试解”中提到，1801年高斯的不定方程的序列值解法依靠解的依赖性。线性不定方程ax=by±1中，a，b是正整数，a不小于b。由可解条件，a与b互素，辗转相除，自然余数1，与附加数1相对应。求出不定方程ax=by±1的解，就可以解出一般常数的不定方程ax=by±c。
（数例二1）中说，“设约简的被除数[乘数]和除数为137和60，而增加或附加数为10”，我们采纳大系数ax约定，紧随附加数10，写成阿耶波多不定方程137x+10=60y。
第一次辗转相除，如（术文1）说，“根据已知的乘数和除数，用（辗转相除法找到的）最大公约数，加以约简”，可约得互素的系数。
再次辗转相除，互素两系数一定求出自然余数1。
根据原有方程137x+10=60y，进行默认的预处理，得到附加数1的137x+1=60y。
2 整除式的构作
由于缺少欧拉那种“x，y代入其他未知数”的变量分析法，婆罗摩笈多只能围绕自然余数1，设立一套构作整除式的法则。利用余数1从三个角度做文章，涉及它的值1，涉及商个数的奇、偶，还有产生余数1的相应除数，构作整除式。
为此，不得不设定严格的前提：如不定方程137x+10=60y附加数为正，紧跟在大系数“ax”之后，形成特定的不定方程表达式。预处理附加数为1，成137x+1=60y，这才可以清点余数1时的商个数，作出加减的判断：奇数时为加，偶数时为减。
于是有（术文2）：“对余数单位1乘以一个所选择的数，使得乘积减去1（或者加上1，当商个数为奇数时），将可以由产生余数单位1的相应除数所整除。”我们称整除式。分母，就是“产生余数单位1的相应除数”，也就是8。分子有两项，由乘积与加、减附加数所组成。
一是乘积：“余数单位1乘以一个所选择的数”，可从所选择的数，谋求整除。
另一项为加、减1，以适应整数对的奇序、偶序，规律是：当商个数为偶数时，减去1，作为主体，写在正文中；当商个数为奇数时，加上1，作为辅助，置于括号内。
注意，不定方程137x+1=60y，余数1的商个数4是偶数，137和60是偶序整数对。这是（术文2）正文的说法，不统计首商0。
取解式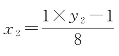
以整除为目标，“我们选9作为选定数”，y2=9，整除得x2=1。
3 余数1商个数的奇偶变动
从阿耶波多不定方程137x+10=60y看，余数1的商个数是2，3，1，1中第4个，4为偶数。这是（术文2）中正文的说法，即不统计首商0，形成“乘积减去1”。
然而，（数例二2）的说法略有改动，承认60=137×0+60的首商0，余数1的商个数变成0，2，3，1，1中第5个，5为奇数。
因此，数例2的商个数为奇数，还是出现1×9-1，即术文中的“乘积减去1”。
相应地，（术文2）中辅助的括号“或者加上1，当商个数为奇数时”，指另外一类奇序整数对。60x+16=13y，两系数辗转相除到自然余数1而止：2y2=3x2+1。商个数为5，奇数，构造出整除式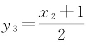
，用的是“加上1”。参见18.4.3。
4 取解式和初解
两系数辗转相除，常数同时参与辗转相除，得到一系列降系数不定方程。利用某个降系数不定方程，取出整数解。
这个取出整数解的式子称为取解式。取解式的解称作初解（初步的解）。
需要回代入这一系列降系数方程，才得到原不定方程的通解和特解。
取解式各有不同，可以与余数0相关，也可以与余数1相关。
整除式
取解，必取“所选择的数”y2=9，才出现x2=1。初解只能写成y2=9和x2=1。
可见，以整除式取解，只利用余数1，与余数0无关。
5 依赖性的应用
最后，婆罗摩笈多依赖137x+1=60y的解，去解出阿耶波多不定方程137x+10=60y。
以x=7，y=16乘10，得x=70，y=160。
再各除以对方系数，得x=70÷60余10，y=160÷137余23。所以x=10，y=23是137x=60y-10的一组最小正整数解。核算：137×10=1370=23×60-10。
可见x=10，y=23是不定方程137x+10=60y的一组特殊解。