4.4 三色差分解法
时曰醇，字清甫，世为嘉定（今上海嘉定）人。
父时铭（1768-1827），嘉庆乙丑（1805年）科进士，嘉庆十九年（1814年）补齐东县（今山东邹平县内），道光元年（1821年）“以催科不力劾罢”，道光七年（1827年）卒于济南寓邸。数学著作有《笔算筹算图》一卷。
时曰醇的生卒年代不见于数学史专著，今据《嘉定县志》本传，知“光绪庚辰（1880年）卒，年七十四”。由此推得其生年为1807年。少时“入监，专治九数”。咸丰辛酉（1861年），丁取忠在武昌为湖北巡抚胡林翼（1812—1861）的幕宾。是年春，时曰醇与丁取忠同客武昌商榷百鸡术，“别后数月乃得通之”。同年重九日，时曰醇成《百鸡术衍》二卷[2]。晚年被聘入广方言馆。其时虽已“年老聋瞽”，仍为“诸生口讲指画，剖毫析芒”。时曰醇的著作还有《今有术申》一卷，《求一术指》一卷，而《百鸡术衍》二卷为其代表作。
《百鸡术衍》二卷是关于三色差分的著作。全书共二十八题，以“旧学商量加邃密，新知培养转深沉”十四字为序，每序有上、下题。上题的旧、学、商三题，题各成组，量加、邃密新、知培养转深沉各成一组，共为六组。相应下题亦分别成组，仍为六组。各上题所给物数相同，值钱数不同，形如
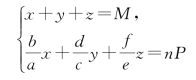
的三元一次不定方程组，其中，a，c，e分别是大物、中物、小物的物数，b，d，f分别是其相应的值钱数，M为共物，nP为共值，a，c，e，b，d，f，M，nP皆为正整数，且
。相应的下题，值钱数相同，物数不同，具有如下形式：
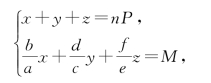
其中，f，d，b为物数，e，c，a为值钱数，n P为共物，M为共值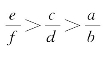
，其余条件同上。
对全书的考察可知，P是
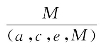
三色差分解法的基本思想是，减少题目未知数的个数，使不定解的问题，转化为确定解的问题，而后求解。
具体步骤是：先设一物为零，使得三色差分化为二色差分。借方程术解得一组解。次由约率加减得一组非负整数解。复由约率加减得一组整数解，使其对应的值钱数，亦皆为正整数。更由通率加减得其全部正整数解。该法的关键是正确地求出约率与通率。
时曰醇的三色差分解法，步骤明确，通行于全书二十八题。
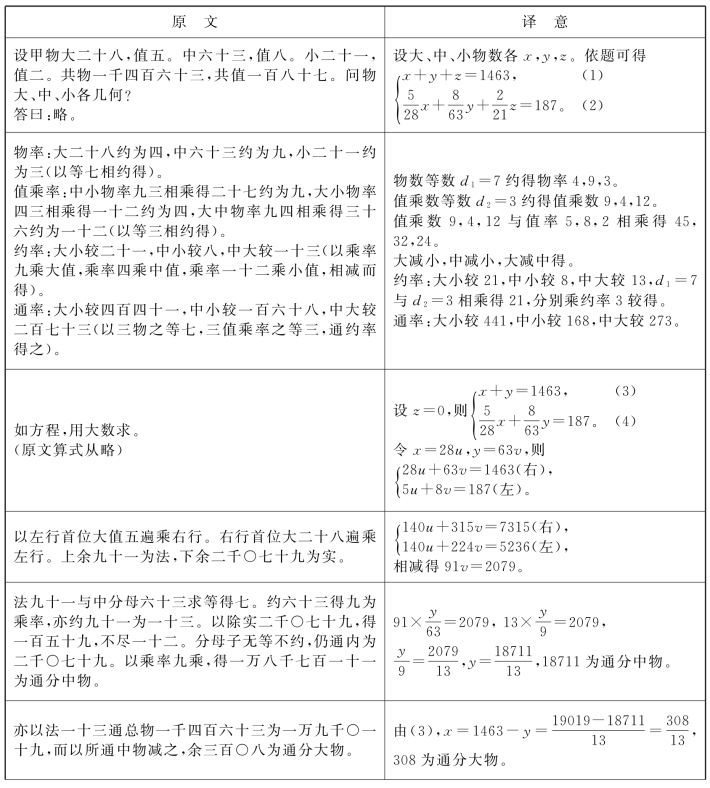
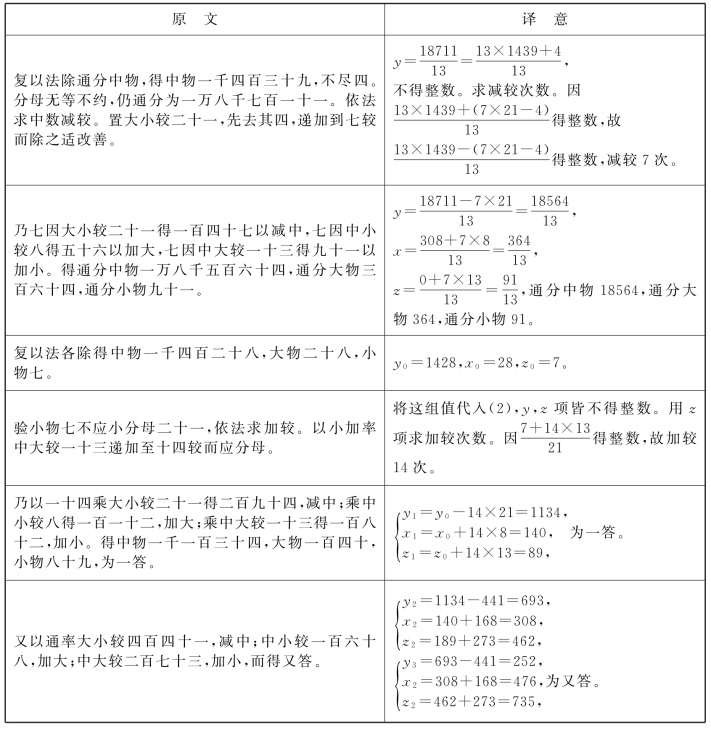
兹录知上题原文，分步解释如下（表4.2）：
表4.2 时曰醇的三色差分释意
续表
丁取忠为《百鸡术衍》（1861年）作序，盛赞时曰醇使百鸡术“灿然大著”，却没有提及骆腾凤术。
时曰醇自序，称丁取忠《数学拾遗》（1851年）“设术与二色方程暗合，乃通法”。而对骆腾凤求一解法，则说：“取笃颇巧，然于较除共较实适尽者不可求，……骆氏盖不知有方程本术也。”
时曰醇说骆腾凤不知有方程本术，这种观点显然不合事实。遇“共较实”恰能被“较”除尽时，只需约去公因子，同样可以用骆腾凤术求解。
为比较起见，我们现在来分析丁取忠、时曰醇的方法。
《数学拾遗》法曰：
先取鸡母鸡雏二色差分，求鸡母原数。置鸡百只，以四归之，得二十五为原母数。以原母减鸡百只，余七十五为原雏数。
丁取忠继以经术鸡翁、母、雏增减率四、七、三损益之，而得三答。
时曰醇《百鸡术衍》造术，则为：
如方程，用鸡雏求，以左行首位雏直一遍乘右行，右行首位雏三遍乘左行，两两相减，上余八为法，下余二百为实。除之得二十五。以母一乘不变，即为鸡母数。以减共鸡一百，余七十五为鸡雏数，乃用翁雏较七减母，母雏较四加翁，母翁较三加雏，得鸡母一十八，鸡翁四，鸡雏七十八，为一答。以各依较数加减而得又答。
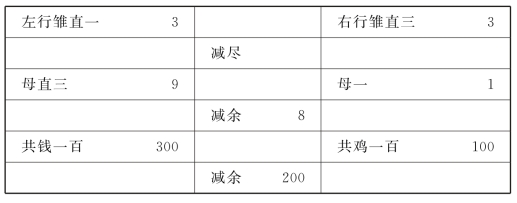
可参见表4.3。
表4.3 时曰醇的三色差分释意
以上两术实质都是假设鸡翁为零，得二元一次方程组
消去z得8y=200，故y=25，其中200为实，8为法。时曰醇取方程组为
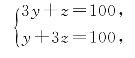
消去z后，所得答数一样。
很明显，上术若遇以法除实不尽时，则不能通过。此时时曰醇另立它术。我们可以通过实例来分析。
《百鸡术衍》卷上第3题为：“设大物一直三，中物三直五，小物五直一，共物一百，共直一百，问物大中小各几何？”用小数求，列方程为
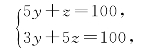
消去z，得11y=200，法除实不尽。此时相当于用消去法将原来的两个方程化为一个二元一次不定方程
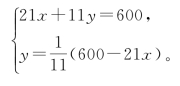
然后以x=1，2，…诸数试算，得x=5时，y为正整数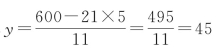
。显然，在这一情况，两者是一样的，都是先化得一个形如ax+by=c的不定方程，所不同者，骆腾凤是用大衍求一术来解此不定方程，而时曰醇则用试算的方法来求解。可见，丁、时法要真正成为通解，还必须求助于大衍求一术。
《百鸡术衍》采用丁取忠设一物为零的方法，所得二色差分借用梅文鼎（1633—1721）《方程论》（1672年）的方法求解，较二色差分本法简明，又首创约率简便算法、通率及其算法、加较减较法，构成三色差分的严谨解法。
作为三色差分的最早记载，百鸡问题给出物数两两互素且共物与共值相等。时曰醇去掉这些限制，使之一般化，进而揭示了“同解”的与“对称”的三色差分，从而提供了构造三色差分的一般方法。时曰醇之前的研究基本上是就题论题，未曾如此全面细致。《百鸡术衍》二卷可以视为三色差分的系统总结。但书中需要求解形如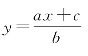
的不定方程，时曰醇未能采用简便方法，而代之以试算，失之简捷。