9.2.2 解形如Z=ma+p=nb+q的一次同余式组
在此基础上，利用两系数“被a和b除所得的余数分别是p和q，这里a＞b”，欧拉发展成为解形如Z=ma+p=nb+q的一次同余式组。
欧拉处理这样一个问题，求一个整数Z，被a和b除所得的余数分别是p和q，这里a＞b，即有Z=ma+p=nb+q。欧拉从第二个方程解，采取了求a，b最大公因数的方法，把a，b辗转相除，求出一系列余数c，d，e，…，直到某一个余数能整除v=p-q为止。从而，欧拉可得
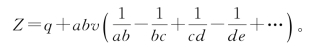
括号中是一个级数，级数的最后一项取决于能整除v的余数。
可能是狄克逊摘录时有所脱漏，作为一个普遍适用的解法，还要两个十分明显的条件：0＜v＜[a，b]和当Z为负值时，用若干个[a，b]减去Z。[a，b]表示a，b的最小公倍数。
在前面形如ma+v=nb的不定方程中，令v=p-q，就得到ma+p=nb+q，可以成为Z=ma+p=nb+q。我们证明如下：
把v=p-q和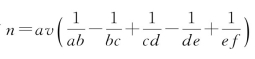
代入不定方程ma+v=nb，得到记Z=ma+p=nb+q，有
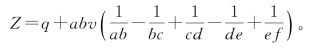
为简化叙述，采用两个数字例子来介绍欧拉的解法。
数例一 为利于比较，选用黄宗宪演算过的秦九韶“推计土功”题，从衍数3800和甲定27得到乘率23的两个互素模a=3800，b=27，即有a＞b，[a，b]=102600。再任取一数56789作Z来核算。56789=14×3800+3589=2103×27+8，于是p=3589，q=8，v=p-q=3589-8=3581。用求a，b最大公因数的方法，把a，b辗转相除，求余数序列：a÷b=3800÷27，余20，令c=20；b÷c=27÷20，余7，令d=7；c÷d=20÷7，余6，令e=6；d÷e=7÷6，余1，令f=1。检查知，余数序列c，d，e，f，…中，只有f=1能整除v=3581，因此，括号中取5项，
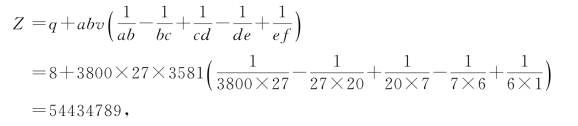
a，b的最小公倍数是102600，54434789-102600×530=56789，正是所设的Z。
数例二 取有公因数4的两个模a=16，b=12，即有a＞b，[a，b]=48。再任取一数89作Z，89=5×16+9=6×12+5，p=9，q=5，v=p-q=9-5=4。把a，b辗转相除，求余数序列：a÷b=16÷12，余4；令c=4。检查知，余数序列c就能整除v=4，因此，括号中取二项，
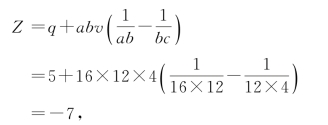
a，b的最小公倍数是48，48×2-7=89，正是所设的Z。此法需要考察v=4的整除，说明注意到同余式组的可解条件问题[1]。